Leetcode 516.最长回文子序列
Leetcode 516.最长回文子序列
题目要求
-
给你一个字符串 s ,找出其中最长的回文子序列,并返回该序列的长度。
-
子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例1:
输入:s = “bbbab”
输出:4
解释:一个可能的最长回文子序列为 “bbbb” 。
示例2:
输入:s = “cbbd”
输出:2
解释:一个可能的最长回文子序列为 “bb” 。
动态规划
动规五部曲
-
确定dp数组(dp table)以及下标的含义
dp[i][j]:下标在[i, j]范围内的字符串的最长回文子序列的长度 -
确定递推公式
- 当s.charAt(i) != s.charAt(j)时,说明当前肯定不是回文串
- dp[i][j] = Math.max(dp[i+1][j], dp[i][j-1])
- 当s.charAt(i) == s.charAt(j)时,说明当前字符相等
- dp[i][j] = dp[i+1][j-1] + 2
- 当s.charAt(i) != s.charAt(j)时,说明当前肯定不是回文串
-
dp数组如何初始化
根据递推公式可以发现,i一直向右移动,j一直向左移动,最终直到i==j时,说明此时只有一个字符,最长回文子序列长度为1
所以初始化时,令dp[i][i] = 1 -
确定遍历顺序
遍历i从下往上遍历,遍历j从左往右遍历 -
举例推导dp数组
- 举例:“cbbd”
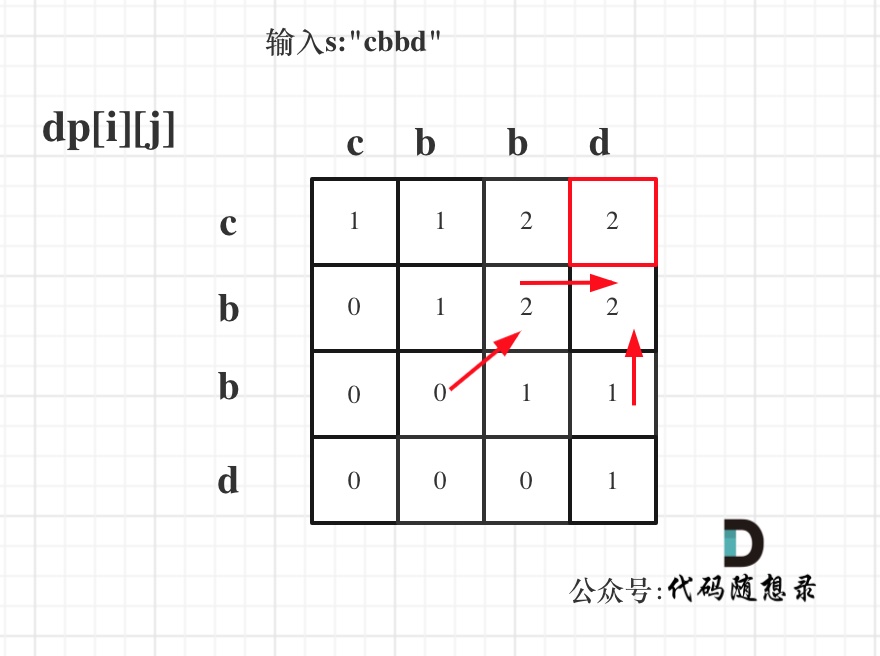
- 举例:“cbbd”
1 | class Solution { |











