Leetcode 72.编辑距离

题目要求

  • 给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

  • 你可以对一个单词进行如下三种操作：

    • 插入一个字符
    • 删除一个字符
    • 替换一个字符

示例1：
输入：word1 = “horse”, word2 = “ros”
输出：3
解释：
horse -> rorse (将 ‘h’ 替换为 ‘r’)
rorse -> rose (删除 ‘r’)
rose -> ros (删除 ‘e’)

示例2：
输入：word1 = “intention”, word2 = “execution”
输出：5
解释：
intention -> inention (删除 ‘t’)
inention -> enention (将 ‘i’ 替换为 ‘e’)
enention -> exention (将 ‘n’ 替换为 ‘x’)
exention -> exection (将 ‘n’ 替换为 ‘c’)
exection -> execution (插入 ‘u’)

动态规划

动规五部曲

  1. 确定dp数组（dp table）以及下标的含义
    dp[i][j]：长度为[0, i - 1]的字符串word1与长度为[0, j - 1]的字符串word2，使得word1和word2相同所需的最小步数

  2. 确定递推公式

    • 当word1[i-1] == word2[j-1]，说明当前字符相等，不需要增删改操作
      • dp[i][j] = dp[i-1][j-1]
    • 当word1[i-1] != word2[j-1]，说明当前字符不等，需要增删改操作（增加相当于删除，所以不需要单独考虑）
      • 删除word1（相当于不考虑word1[i-1]）: dp[i][j] = dp[i-1][j] + 1 (dp[i-1][j]就相当于把word1[i-2]删了，后面多加了一步)
      • 删除word2: dp[i][j] = dp[i][j-1] + 1
      • 替换: dp[i][j] = dp[i-1][j-1] + 1
      • 取三者的最小值

  3. dp数组如何初始化
    当其中一个字符串为空时，另一个字符串有多长删多长

    • dp[i][0] = i
    • dp[0][j] = j

  4. 确定遍历顺序
    从前往后遍历

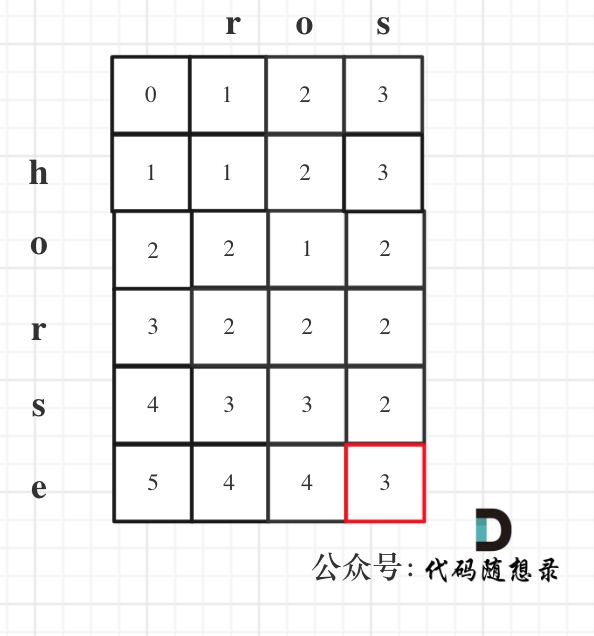
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int minDistance(String word1, String word2) {
        int[][] dp = new int[word1.length() + 1][word2.length() + 1];

        for (int i = 1; i <= word1.length(); i++) {
            dp[i][0] = i;
        }

        for (int j = 1; j <= word2.length(); j++) {
            dp[0][j] = j;
        }

        for (int i = 1; i <= word1.length(); i++) {
            for (int j = 1; j <= word2.length(); j++) {
                if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
                    dp[i][j] = dp[i - 1][j - 1];
                }else {
                    dp[i][j] = Math.min(dp[i-1][j-1], Math.min(dp[i-1][j], dp[i][j-1])) + 1;
                }
            }
        }

        return dp[word1.length()][word2.length()];
    }
}