Leetcode 392.判断子序列

题目要求

  • 给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

  • 字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

示例1：
输入：s = “abc”, t = “ahbgdc”
输出：true

示例2：
输入：s = “axc”, t = “ahbgdc”
输出：false

动态规划

动规五部曲
其实就是最长公共子序列，只不过需要看这个子序列是不是s

  1. 确定dp数组（dp table）以及下标的含义
    dp[i][j]：长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]

  2. 确定递推公式

    • 如果text1[i - 1] == text2[j - 1]，说明当前字符相等，最长公共子序列长度加1
      • dp[i][j] = dp[i - 1][j - 1] + 1
    • 如果text1[i - 1] != text2[j - 1]，说明当前字符不等，最长公共子序列长度为去掉其中一个字符后的最大值
      • dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])

  3. dp数组如何初始化
    dp数组所有元素都初始化为0

  4. 确定遍历顺序
    从前往后遍历

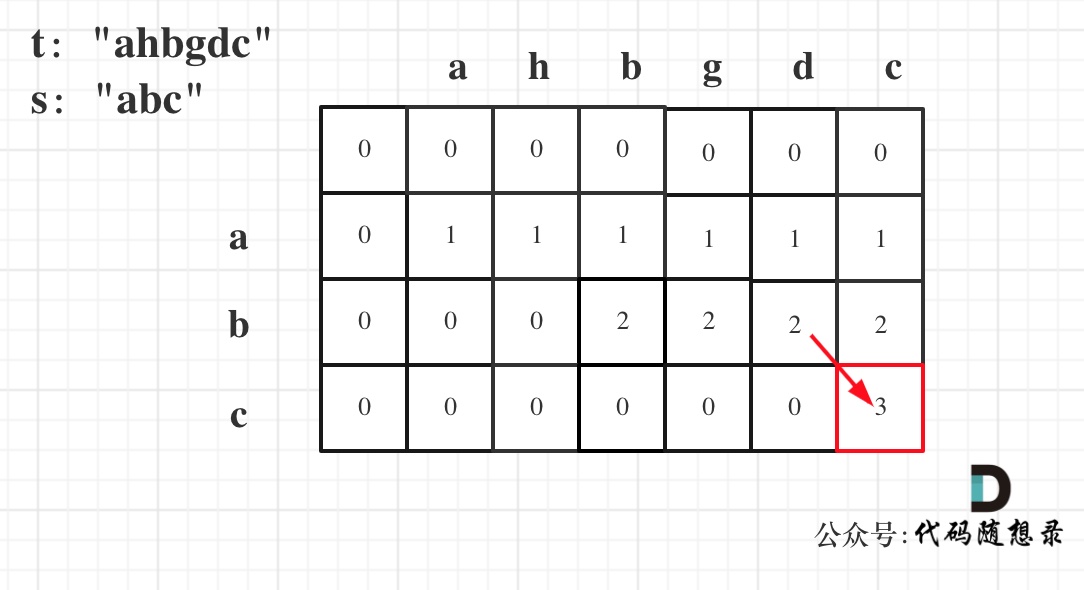
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public boolean isSubsequence(String s, String t) {
        if (s.length() == 0) return true;
        if (t.length() == 0) return false;

        int[][] dp = new int[s.length() + 1][t.length() + 1];

        for (int i = 1; i <= s.length(); i++) {
            for (int j = 1; j <= t.length(); j++) {
                if (s.charAt(i-1) == t.charAt(j-1)) {
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                }else
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }

        boolean res = dp[s.length()][t.length()] == s.length();

        return res;
    }
}