Leetcode 674.最长连续递增序列

题目要求

  • 给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。

  • 连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], …, nums[r - 1], nums[r]] 就是连续递增子序列。

示例1：
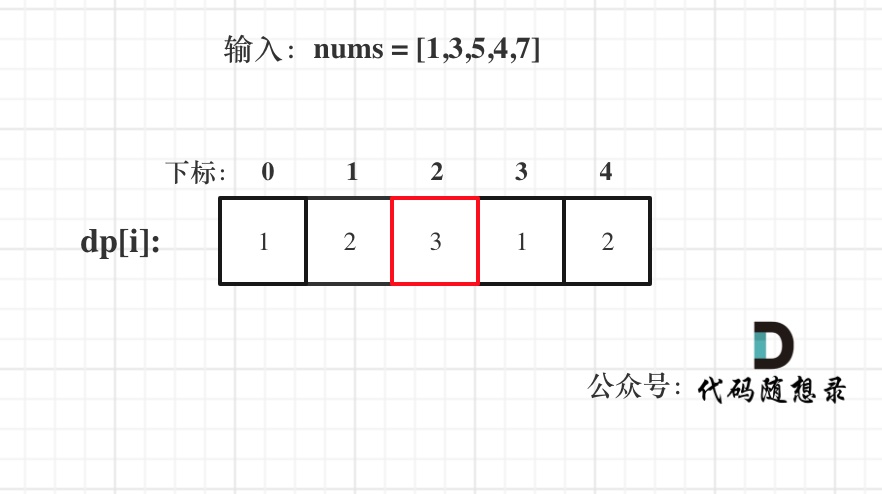
输入：nums = [1,3,5,4,7]
输出：3
解释：最长连续递增序列是 [1,3,5], 长度为3。
尽管 [1,3,5,7] 也是升序的子序列, 但它不是连续的，因为 5 和 7 在原数组里被 4 隔开。

示例2：
输入：nums = [2,2,2,2,2]
输出：1
解释：最长连续递增序列是 [2], 长度为1。

动态规划

动规五部曲

  1. 确定dp数组（dp table）以及下标的含义
    dp[i]：以nums[i]结尾的最长递增子序列的长度

  2. 确定递推公式

    • 对于元素nums[i]，最长连续递增序列只有两种情况：
      1. 不以nums[i]结尾
      2. 以nums[i]结尾
    • 如果不以nums[i]结尾，说明最长连续递增序列在nums[0…i-1]中，即dp[i-1]
    • 以nums[i]结尾，则从nums[i]从后往前遍历，统计nums[i]>nums[i-1]的个数，即为以nums[i]结尾的最长连续递增序列的长度，使用dp[i]记录
    • 最后取最大值即可：dp[i] = Math.max(dp[i], dp[i-1])

  3. dp数组如何初始化
    dp数组每个元素初始化为1，因为每个元素单独成一个子序列，长度至少为1

  4. 确定遍历顺序
    外层从前往后遍历，内层从后往前遍历统计以nums[i]结尾的最长连续递增序列的长度。

  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];

        for (int i = 0; i < nums.length; i++) {
            dp[i] = 1;
        }
        for (int i = 1; i < nums.length; i++) {
            for (int j = i; j > 0; j--) {
                if (nums[j] > nums[j-1]) {
                    dp[i]++;
                }else {
                    break;
                }
            }
            dp[i] = Math.max(dp[i],dp[i-1]);
        }
        return dp[nums.length - 1];
    }
}

代码随想录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
     * 1.dp[i] 代表当前下标最大连续值
     * 2.递推公式 if（nums[i+1]>nums[i]） dp[i+1] = dp[i]+1
     * 3.初始化 都为1
     * 4.遍历方向，从其那往后
     * 5.结果推导 。。。。
     * @param nums
     * @return
     */
    public static int findLengthOfLCIS(int[] nums) {
        int[] dp = new int[nums.length];
        for (int i = 0; i < dp.length; i++) {
            dp[i] = 1;
        }
        int res = 1;
	    //可以注意到，這邊的 i 是從 0 開始，所以會出現和卡哥的C++ code有差異的地方，在一些地方會看到有 i + 1 的偏移。
        for (int i = 0; i < nums.length - 1; i++) {
            if (nums[i + 1] > nums[i]) {
                dp[i + 1] = dp[i] + 1;
            }
            res = res > dp[i + 1] ? res : dp[i + 1];
        }
        return res;
    }