Leetcode 188.买卖股票的最佳时机IV

题目要求

  • 给你一个整数数组 prices 和一个整数 k ，其中 prices[i] 是某支给定的股票在第 i 天的价格。

  • 设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说，你最多可以买 k 次，卖 k 次。

  • 注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1：
输入：k = 2, prices = [2,4,1]
输出：2
解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例2：
输入：k = 2, prices = [3,2,6,5,0,3]
输出：7
解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

动态规划

动规五部曲
本题与Leetcode123.买卖股票的最佳时机III类似，不过本题是最多可以完成 k 笔交易，而不是最多完成两笔交易

  1. 确定dp数组（dp table）以及下标的含义
    一天一共就有五个状态，
    0：没有操作 （其实我们也可以不设置这个状态）
    j % 2 != 0：第（j + 1）/ 2次持有股票
    j % 2 == 0：第j / 2次不持有股票
    dp[i][j]中 i表示第i天，j为 [0 - 2*k] 2k个状态，dp[i][j]表示第i天状态j所剩最大现金。

  2. 确定递推公式

    1. 没有操作
      • dp[i][0] = dp[i-1][0]
    2. j % 2 == 0（第j / 2次不持有股票）：以前不持有或今天卖了
      • dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] + prices[i])
    3. j % 2 != 0（第（j + 1）/ 2次持有股票）：以前持有或今天买了
      • dp[i][j] = max(dp[i-1][j], dp[i-1][j-1] - prices[i])

  3. dp数组如何初始化
    第0天没有操作：dp[0][0] = 0
    第0天持有股票：dp[0][j] = -prices[0]（j为奇数）
    第0天不持有股票：dp[0][j] = 0（j为偶数）

  4. 确定遍历顺序
    从前往后遍历。

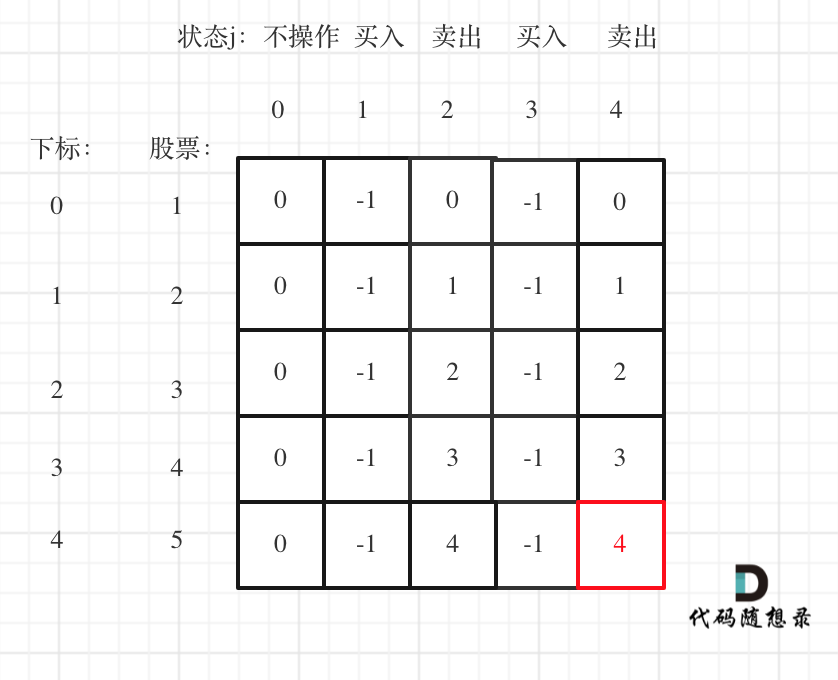
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
    public int maxProfit(int k, int[] prices) {
        int[][] dp = new int[prices.length][2*k + 1];
        
        for (int j = 0; j <= 2*k; j++) {
            if (j % 2 == 0) {
                dp[0][j] = 0;
            } else {
                dp[0][j] = -prices[0];
            }
        }

        for (int i = 1; i < prices.length; i++) {
            dp[i][0] = dp[i-1][0];
            for (int j = 1; j <= 2*k; j++) {
                if (j % 2 == 0) {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-1] + prices[i]);
                }else {
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-1] - prices[i]);
                }
            }
        }

        return dp[prices.length - 1][2*k];
    }
}