Leetcode 322.零钱兑换

题目要求

  • 给你一个整数数组 coins ，表示不同面额的硬币；以及一个整数 amount ，表示总金额。

  • 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额，返回 -1 。

你可以认为每种硬币的数量是无限的。

示例1：
输入：coins = [1, 2, 5], amount = 11
输出：3
解释：11 = 5 + 5 + 1

示例2：
输入：coins = [2], amount = 3
输出：-1

示例 3：
输入：coins = [1], amount = 0
输出：0

动态规划

动规五部曲
这道题跟完全背包问题类似，只不过是求组合数而不是最大价值。

  1. 确定dp数组（dp table）以及下标的含义
    dp[j]表示凑成总金额j的最少硬币个数

  2. 确定递推公式
    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1)

  3. dp数组如何初始化
    dp[0] = 0
    因为后续要比较取最小值，所以其他值初始化为一个较大的数——Integer.MAX_VALUE

  4. 确定遍历顺序
    正着遍历，物品可以重复使用

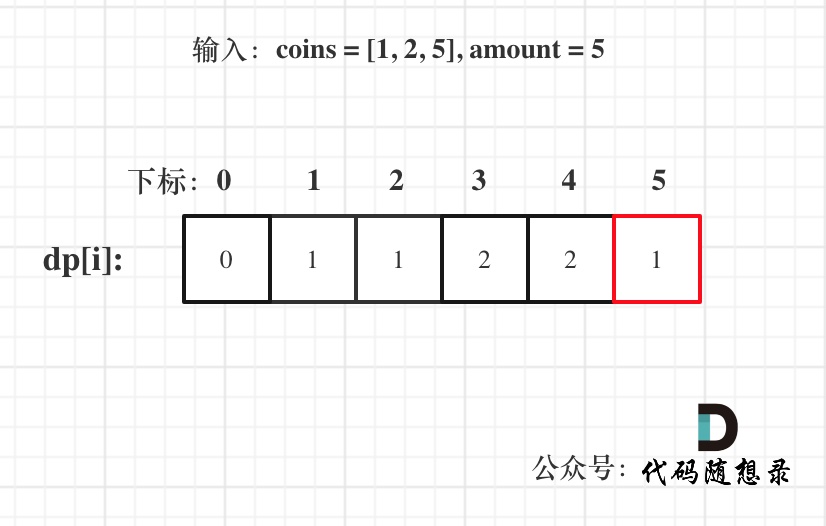
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp = new int[amount + 1];

        dp[0] = 0;
        for (int i = 1; i <= amount; i++) {
            dp[i] = Integer.MAX_VALUE;
        }

        for (int i = 0; i < coins.length; i++) {
            for (int j = coins[i]; j <= amount; j++) {
                // 只有当dp[j - coins[i]]不为Integer.MAX_VALUE时，才有比较的必要
                if (dp[j - coins[i]] != Integer.MAX_VALUE) {
                    dp[j] = Math.min(dp[j], dp[j - coins[i]] + 1);
                }
            }
        }

        if (dp[amount] == Integer.MAX_VALUE) return -1;
        return dp[amount];
    }
}