完全背包问题

题目要求

  • 有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个（也就是可以放入背包多次），求解将哪些物品装入背包里物品价值总和最大。

  • 完全背包和01背包问题唯一不同的地方就是，每种物品有无限件。

示例：
背包最大重量为4，物品为：

物品 重量 价值
物品0 1 15
物品1 3 20
物品2 4 30

每件商品都有无限个，问背包能背的物品最大价值是多少？

动态规划

动规五部曲
其实就是每个物品可以重复取，之前内部遍历j的时候倒序遍历就是为了防止物品重复使用，现在正序遍历即可

  1. 确定dp数组（dp table）以及下标的含义
    dp[i][j]表示前i件物品放入容量为j的背包中能获得的最大价值。

  2. 确定递推公式
    两种情况：放物品i和不放物品i。

    • 不放：dp[i][j] = dp[i-1][j]
    • 放：dp[i][j] = dp[i][j - weight[i]] + value[i]

  3. dp数组如何初始化
    初始化第一行和第一列，第一列全为0，第一行在放得下物品0之前全为0

  4. 确定遍历顺序
    正着遍历，物品可以重复使用

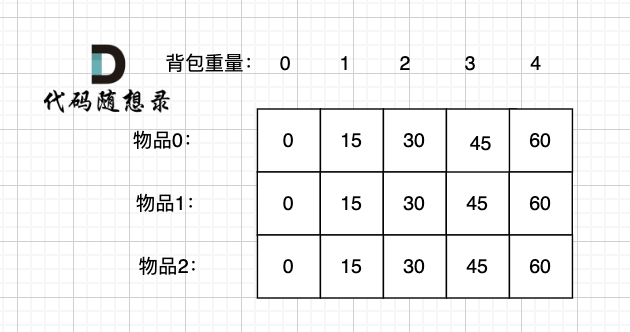
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int bagWeight = scanner.nextInt();

        int[] weight = new int[n];
        int[] value = new int[n];

        for (int i = 0; i < n; i++) {
            weight[i] = scanner.nextInt();
            value[i] = scanner.nextInt();
        }

        int[][] dp = new int[n][bagWeight + 1];

        // 初始化
        for (int j = weight[0]; j <= bagWeight; j++) {
            dp[0][j] = dp[0][j - weight[0]] + value[0];
        }

        // 动态规划
        for (int i = 1; i < n; i++) {
            for (int j = 0; j <= bagWeight; j++) {
                if (j < weight[i]) {
                    dp[i][j] = dp[i - 1][j];
                } else {
                    dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
                }
            }
        }

        System.out.println(dp[n - 1][bagWeight]);
        scanner.close();
    }
}