Leetcode 474.一和零

题目要求

  • 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。

  • 请你找出并返回 strs 的最大子集的长度，该子集中 最多 有 m 个 0 和 n 个 1 。

  • 如果 x 的所有元素也是 y 的元素，集合 x 是集合 y 的 子集 。

示例 1:
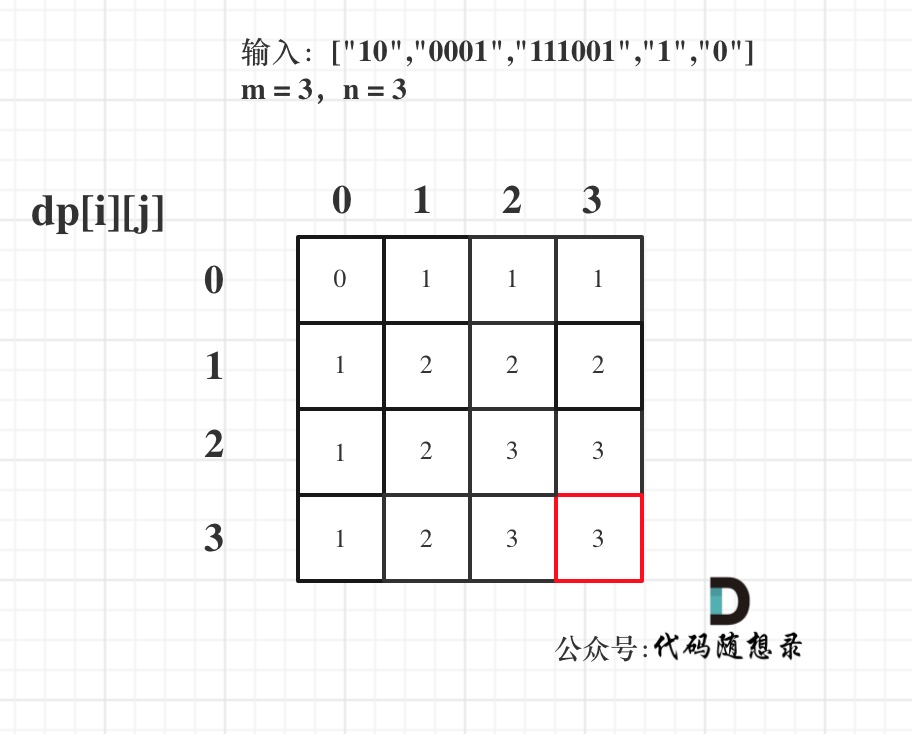
输入：strs = [“10”, “0001”, “111001”, “1”, “0”], m = 5, n = 3
输出：4
解释：最多有 5 个 0 和 3 个 1 的最大子集是 {“10”,“0001”,“1”,“0”} ，因此答案是 4 。
其他满足题意但较小的子集包括 {“0001”,“1”} 和 {“10”,“1”,“0”} 。{“111001”} 不满足题意，因为它含 4 个 1 ，大于 n 的值 3 。

示例 2：
输入：strs = [“10”, “0”, “1”], m = 1, n = 1
输出：2
解释：最大的子集是 {“0”, “1”} ，所以答案是 2 。

动态规划

动规五部曲
其实就是从一（二）维数组上升到二（三）维数组的过程。

  1. 确定dp数组（dp table）以及下标的含义
    dp[j][k]表示在使用j个0和k个1的情况下，能够组成的最大子集的长度。

  2. 确定递推公式
    两种情况：放strs[i]和不放strs[i]。

    • 不放：dp[j][k] = dp[j][k]
    • 放：dp[j][k] = dp[j - num0[i]][k - num1[i]] + 1

  3. dp数组如何初始化
    dp[0][0] = 0，其他元素初始化为0。

  4. 确定遍历顺序
    倒序遍历，防止元素重复使用

  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        // 统计每个字符串中0和1的个数
        int[] num0 = new int[strs.length];
        int[] num1 = new int[strs.length];

        for (int i = 0; i < strs.length; i++) {
            for (int j = 0; j < strs[i].length(); j++) {
                if (strs[i].charAt(j) == '0') {
                    num0[i]++;
                }else if (strs[i].charAt(j) == '1') {
                    num1[i]++;
                }
            }
        }

        int[][] dp = new int[m + 1][n + 1];

        for (int i = 0; i < strs.length; i++) {
            for (int j = m; j >= num0[i] ; j--) {
                for (int k = n; k >= num1[i]; k--) {
                    dp[j][k] = Math.max(dp[j][k], dp[j - num0[i]][k - num1[i]] + 1);
                }
            }
        }
        return dp[m][n];
    }
}