Leetcode 494.目标和

题目要求

  • 给你一个非负整数数组 nums 和一个整数 target 。

  • 向数组中的每个整数前添加 ‘+’ 或 ‘-’ ，然后串联起所有整数，可以构造一个 表达式 ：

  • 例如，nums = [2, 1] ，可以在 2 之前添加 ‘+’ ，在 1 之前添加 ‘-’ ，然后串联起来得到表达式 “+2-1” 。

  • 返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。

示例 1:
输入：nums = [1,1,1,1,1], target = 3
输出：5
解释：一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3

示例 2：
输入：nums = [1], target = 1
输出：1

动态规划

动规五部曲
本题可以跟以前一样，将所有数分为两个集合，一边是加法集合left，一边是减法集合right。
则left + right = sum, left - right = target
从而可以得到left = (target + sum) / 2
这样就与前面几道题类似了

  1. 确定dp数组（dp table）以及下标的含义
    dp[j]代表填满j（包括j）这么大容积的包，有dp[j]种方法

  2. 确定递推公式
    dp数组递推公式为：dp[j] += dp[j - nums[i]]

  3. dp数组如何初始化
    dp[0] = 1

  4. 确定遍历顺序
    倒序遍历

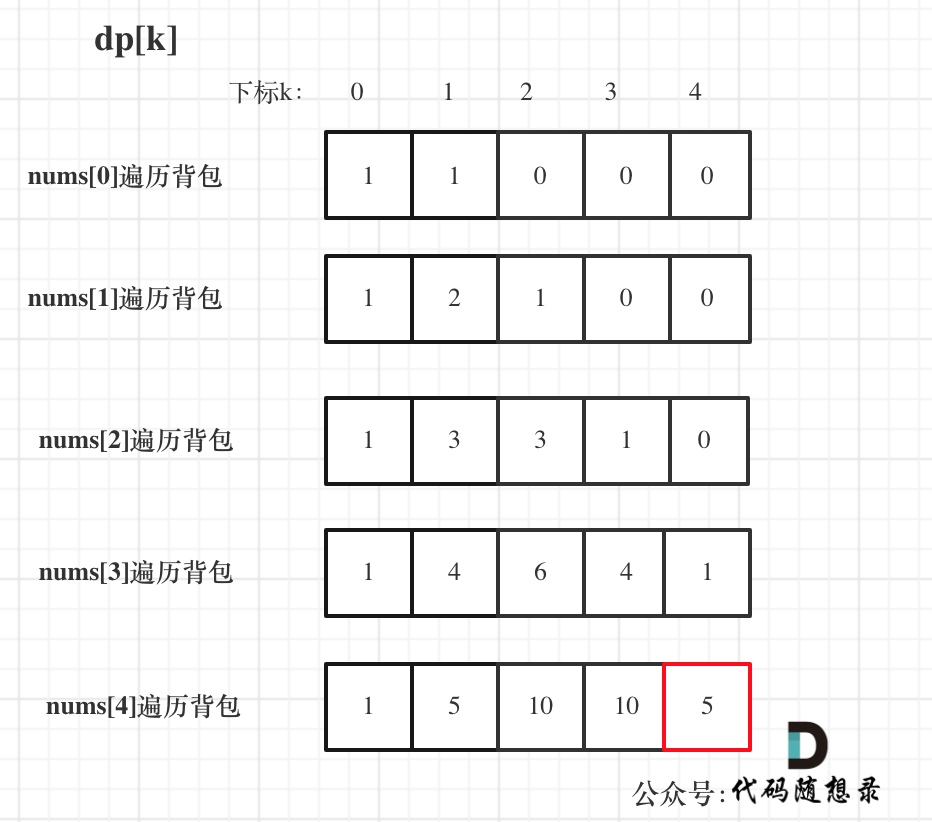
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int findTargetSumWays(int[] nums, int target) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
        }

        //如果target的绝对值大于sum，那么是没有方案的
        if (Math.abs(target) > sum) return 0;
        //如果(target+sum)除以2的余数不为0，也是没有方案的
        if ((target + sum) % 2 == 1) return 0;
        
        int left = (sum + target) / 2;
        int[] dp = new int[left + 1];
        dp[0] = 1;
        for (int i = 0; i < nums.length; i++) {
            for (int j = left; j >= nums[i]; j--) {
                dp[j] += dp[j-nums[i]];
            }
        }

        return dp[left];
    }
}