Leetcode 416.分割等和子集

题目要求

  • 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

示例 1:
输入：nums = [1,5,11,5]
输出：true
解释：数组可以分割成 [1, 5, 5] 和 [11] 。

示例 2：
输入：nums = [1,2,3,5]
输出：false
解释：数组不能分割成两个元素和相等的子集。

动态规划

动规五部曲
本题相当于weight[i] = value[i] = nums[i]，求是否存在dp[sum / 2] = sum / 2。

  1. 确定dp数组（dp table）以及下标的含义
    dp[j]代表容量为j的背包，能装下的最大价值。

  2. 确定递推公式
    dp数组递推公式为：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
    如果dp[i] = sum/2，那么就说明可以分割成两个子集。

  3. dp数组如何初始化
    dp[0] = nums[0]

  4. 确定遍历顺序
    倒序遍历是为了保证物品i只被放入一次！。因为如果一旦正序遍历了，那么物品0就会被重复加入多次！

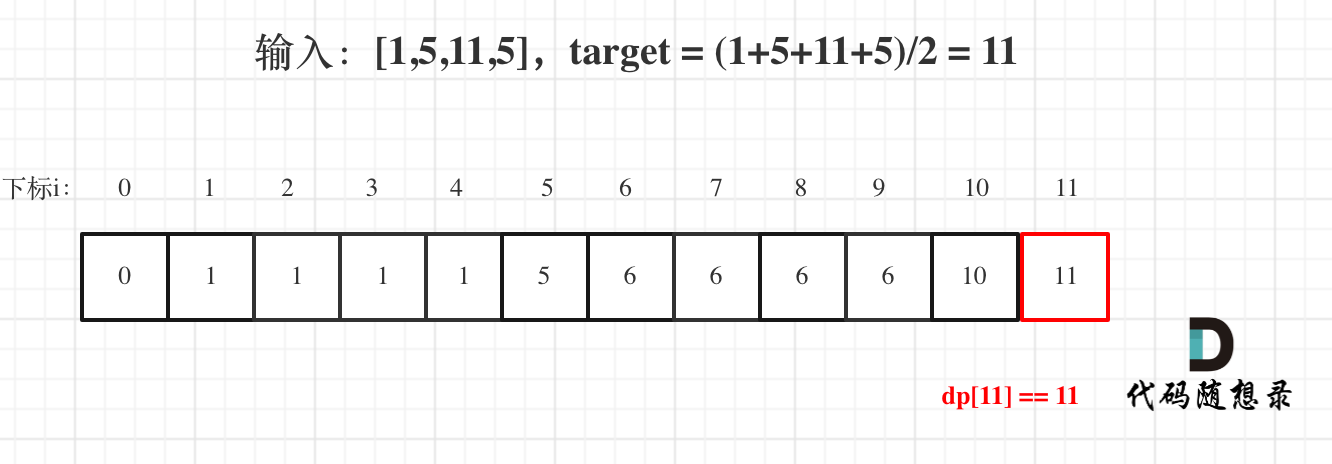
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public boolean canPartition(int[] nums) {
        int sum = 0;
        for (int i = 0; i < nums.length; i++) {
            sum += nums[i];
        }

        // 如果总和是奇数，那么不可能分割成两个相等的子集
        if (sum % 2 != 0) {
            return false;
        }

        int[] dp = new int[sum / 2 + 1];
        for (int i = 0; i < nums.length; i++) {
            for (int j = sum / 2; j >= nums[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);
            }
        }
        return dp[sum / 2] == sum / 2;
    }
}