一维数组求解01背包问题

题目要求

  • 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

示例 1:
背包最大重量为4。

物品为：

物品 重量 价值
物品0 1 15
物品1 3 20
物品2 4 30

问背包能背的物品最大价值是多少？

动态规划

动规五部曲

  1. 确定dp数组（dp table）以及下标的含义
    dp[j]代表的是背包最大重量为j时的最大价值

  2. 确定递推公式
    二维dp数组递推公式为：dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])
    我们可以发现第i行的dp[i][j]只依赖于第i-1行的dp[i-1][j]和dp[i-1][j-weight[i]]，因此可以将二维数组优化为一维数组
    递推公式变为：dp[j] = max(dp[j], dp[j-weight[i]] + value[i])

  3. dp数组如何初始化
    dp[j]表示容量为j的背包，所背的物品价值可以最大为dp[j]，那么dp[0]就应该是0，因为背包容量为0所背的物品的最大价值就是0。
    那么dp数组除了下标0的位置，初始为0，其他下标应该初始化多少呢？
    看一下递归公式：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    dp数组在推导的时候一定是取价值最大的数，如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
    这样才能让dp数组在递归公式的过程中取的最大的价值，而不是被初始值覆盖了。

  4. 确定遍历顺序
    倒序遍历是为了保证物品i只被放入一次！。但如果一旦正序遍历了，那么物品0就会被重复加入多次！

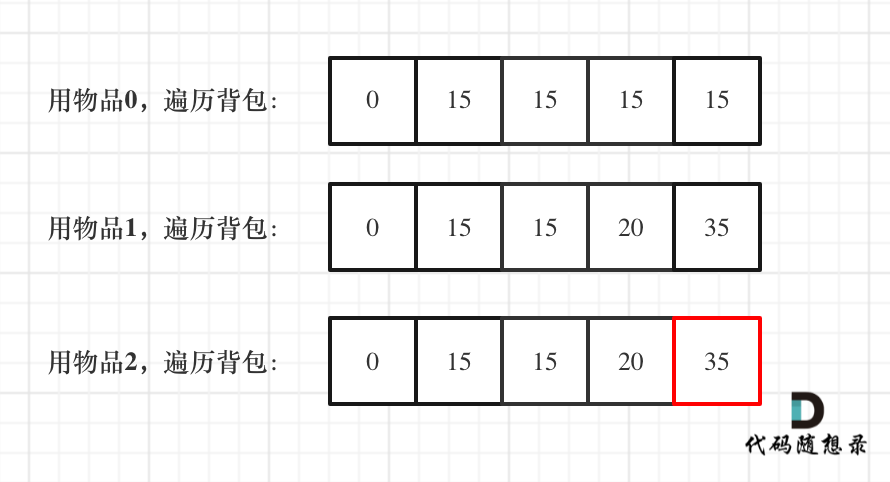
  5. 举例推导dp数组

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int bagweight = scanner.nextInt();

        // 初始化物品重量和价值数组
        int[] weight = new int[n];
        int[] value = new int[n];

        for (int i = 0; i < n; ++i) {
            weight[i] = scanner.nextInt();
        }
        for (int j = 0; j < n; ++j) {
            value[j] = scanner.nextInt();
        }

        // 初始化dp数组
        int[] dp = new int[bagweight + 1];


        for (int i = 0; i < n; i++) {
            for (int j = bagweight; j >= weight[i]; j--) {
                    // 如果背包容量大于等于当前物品重量，则可以选择放入或不放入该物品
                    // 不放入物品i：dp[j]
                    // 放入物品i：dp[j - weight[i]] + value[i]
                    dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
                }
            }
        }
      
        System.out.println(dp[bagweight]);
}