Leetcode 96.不同的二叉搜索树

题目要求

  • 给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

示例 1:

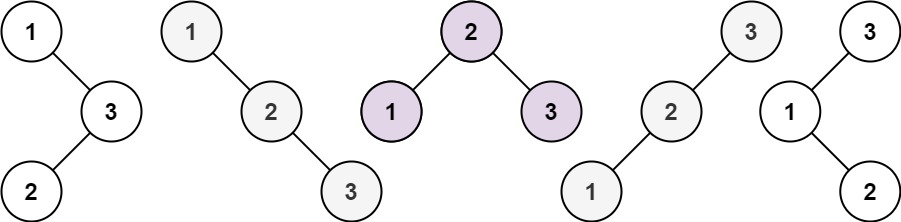
输入：n = 3
输出：5

示例 2:
输入：n = 1
输出：1

动态规划

动规五部曲

  1. 确定dp数组（dp table）以及下标的含义
    dp[i]代表的是i个节点组成的二叉搜索树的种数

  2. 确定递推公式
    假设给定i，那么根节点可以是1、2、3、…i
    对于固定的根节点，左子树和右子树一共剩余i-1个数，假设左子树有j个节点，那么右子树就有i-1-j个节点
    需要注意的是，节点个数为j的情况其实就是dp[j]，虽然数值不一样，但是构造方式相同，因为所有数字都是互不相同的
    所以对于每个根节点都有dp[j] * dp[i - 1 - j]种构造方式
    因此递推公式为：dp[i] = dp[0] * dp[i - 1] + dp[1] * dp[i - 2] + … + dp[i - 1] * dp[0]

  3. dp数组如何初始化
    dp[0] = 1（空树）
    dp[1] = 1（只有一个节点的树）

  4. 确定遍历顺序
    i从2到n，j从0到i-1

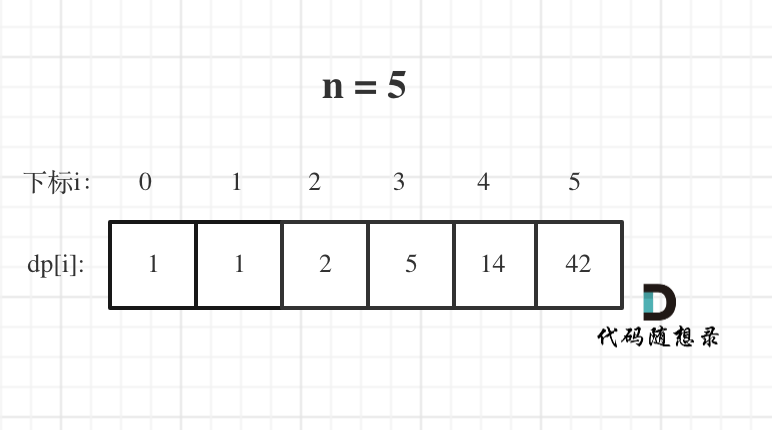
  5. 举例推导dp数组
    当n=10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution {
    public int numTrees(int n) {
        int[] dp = new int[n + 1];
        for (int i = 0; i <= n; i++) {
            dp[i] = 0;
        }
        dp[0] = 1;
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 0; j < i; j++) {
                dp[i] += dp[j] * dp[i - j - 1];
            }
        }
        return dp[n];
    }
}