Leetcode 343.整数拆分

题目要求

  • 给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

  • 返回 你可以获得的最大乘积 。

示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。

示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。

动态规划

动规五部曲

  1. 确定dp数组（dp table）以及下标的含义
    dp[i]给定的正整数i拆分后的最大乘积

  2. 确定递推公式
    假设拆分的其中一个数为j，那么：
    拆分成两个数：dp[i] = j * (i - j)
    拆分成两个数以上：dp[i] = j * dp[i - j]

  3. dp数组如何初始化
    dp[0]无意义
    dp[1]无意义
    dp[2] = 1（只有一种拆法）

  4. 确定遍历顺序
    i从3到n，j从1到i-1

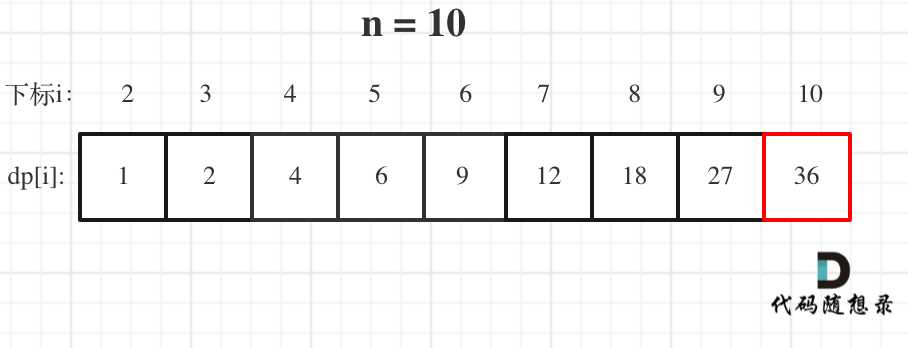
  5. 举例推导dp数组
    当n=10

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int integerBreak(int n) {
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 0;
        dp[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j < i; j++) {
                // 这里相当于dp[i] = Math.max(dp[i], j * (i - j), j * dp[i - j]);
                // 之所以要比较dp[i]，是因为我们要得到的是i固定后dp[i]的最大值
                // 也就是在所有可能的拆分中，取最大的乘积，dp[i]代表的是之前的拆分情况，所以也要参与比较
                dp[i] = Math.max(dp[i], j * (i - j));
                dp[i] = Math.max(dp[i], j * dp[i - j]);
            }
        }
        return dp[n];
    }
}