HGNN+:General Hypergraph Neural Networks

一、论文总结

论文《HGNN+: General Hypergraph Neural Networks》提出了一种通用的超图神经网络框架 HGNN+，以增强超图结构中节点表示学习的灵活性和性能。以下是对该论文的总结：

1.1 背景与动机

超图（Hypergraph）能更好地建模多元关系（如一对多、多对多）问题。然而，现有的超图神经网络（HGNN）方法在灵活性和表达能力方面存在两个主要问题：

  1. 缺乏对高阶关系建模的精细控制，因为大多数方法只关注边聚合，不考虑边内部结构；
  2. 更新机制固定，无法适应不同任务，限制了模型泛化能力。

1.2 HGNN+ 的核心思想

HGNN+ 旨在提供一个可学习的、通用的框架，能够统一现有的超图神经网络，并具备更强的表达能力。其主要特点包括：

1.2.1 双向传播结构

  • 模型在节点-边-节点之间执行双向信息传递；
  • 使用可学习的加权聚合函数来灵活控制信息流动方向和强度。

1.2.2 模块化设计

HGNN+ 将信息传播分解为三类函数：

  • 节点到边聚合（Node2Edge）
  • 边表示更新（EdgeUpdate）
  • 边到节点聚合（Edge2Node）

每个模块都可以用不同的可学习函数实现，从而提高模型的表达能力。

1.2.3 兼容现有方法

HGNN+ 是一个上层框架，可以在其参数设定下还原现有的 HGNN 方法（如HGNN、HyperGCN、HCHA等），从而说明其为一个通用超图神经网络框架。

1.3 实验结果

  • 在多个数据集（如Cora、Citeseer、DBLP等）上进行了节点分类任务；
  • 与现有超图方法和图神经网络方法相比，HGNN+ 在大多数情况下都取得了更好的性能；
  • 进一步分析展示了 HGNN+ 在建模复杂关系结构时的优势。

1.4 总结与贡献

  1. 提出了一种通用、可学习的超图神经网络框架 HGNN+；
  2. 支持现有HGNN方法的统一表达；
  3. 提高了模型在多种任务上的适应性和性能；
  4. 为未来设计更强大HGNN模型提供了基础框架。

二、超图学习目标函数

公式 (1) 出现在 第 3 节 PRELIMINARIES OF HYPERGRAPHS 中，是 HGNN+ 建模超图学习任务的目标函数（Objective Function），用于形式化顶点分类任务。原始公式如下：

arg⁡min⁡f[Remp(f)+Ω(f)](1)\arg\min_f \left[ R_{\text{emp}}(f) + \Omega(f) \right] \tag{1}

2.1 公式结构解读

这是一个典型的正则化目标函数，它由两项组成：

项目 含义 作用
Remp(f)R_{\text{emp}}(f) empirical risk（经验风险） 模型在训练数据上的误差，通常是交叉熵损失等监督学习损失
Ω(f)\Omega(f) regularization term（正则项） 用于鼓励模型输出在超图结构上平滑一致性，即相邻节点应有相似预测结果

目标是学习一个函数 ff，在不牺牲准确率的前提下，使得其预测结果与超图结构中的高阶连接关系保持一致。

2.2 正则项 Ω(f)\Omega(f) 的具体形式（见公式 (2)）

论文进一步在公式 (2) 中定义了 Ω(f)\Omega(f) 的计算方式，用于刻画超图中节点间的“平滑性”：

Ω(f)=12∑e∈E∑{u,v}⊆ew(e)d(e)H(u,e)H(v,e)(f(u)d(u)−f(v)d(v))2\Omega(f) = \frac{1}{2} \sum_{e \in E} \sum_{\{u, v\} \subseteq e} \frac{w(e)}{d(e)} H(u, e) H(v, e) \left( \frac{f(u)}{\sqrt{d(u)}} - \frac{f(v)}{\sqrt{d(v)}} \right)^2

这个公式表达了：

如果两个节点 uu 和 vv 同属于某个超边 ee，并且它们在该超边中的权重较高，那么它们的预测结果 f(u),f(v)f(u), f(v) 应该尽量接近。

换句话说，同一高阶关系下的节点，其标签/表示应尽可能一致。

2.3 公式 (1) 在整个模型中的意义

它是整个 HGNN+ 表征学习任务的理论出发点，强调两点：

  1. 监督学习目标（对已知标签节点做出准确预测）；
  2. 结构一致性（利用超图结构鼓励节点预测的连贯性和平滑性）。

HGNN+ 后续的超图卷积操作（无论是光谱还是空间）本质上都是在设计一种神经网络层，使得最终的预测结果 ff 能够优化这个目标函数。

2.4 举例

假如你在做文献分类任务，每个节点是一个论文，超边是共同作者或共同关键词构成的群组。

  • Remp(f)R_{\text{emp}}(f)：希望你的模型能正确预测训练集中文章的类别；
  • Ω(f)\Omega(f)：希望那些有共同作者/关键词的文章（在同一个超边里）有相似的类别预测。

2.5 小结

公式 (1) 是 HGNN+ 的核心优化目标，它统一了监督损失和结构平滑性约束，使得模型不仅拟合标签，而且能有效利用超图中的高阶结构信息。这种结构感知式正则化是超图学习相较传统图学习的关键优势之一。

三、HGNN+ 超图建模

3.1 超边组的构建

从零开始生成超图的情况可以分为三种情形，即具有图结构的数据、没有图结构的数据以及具有多模态/多类型表示的数据。本文介绍了三种超边生成策略，分别是使用成对边、k kk-hop和特征空间中的邻居：

  • 使用成对边和k kk-hop的方法用于从具有图结构的数据中生成超边组
  • 使用特征空间中的邻居的方法用于从没有图结构的数据中生成超边组。

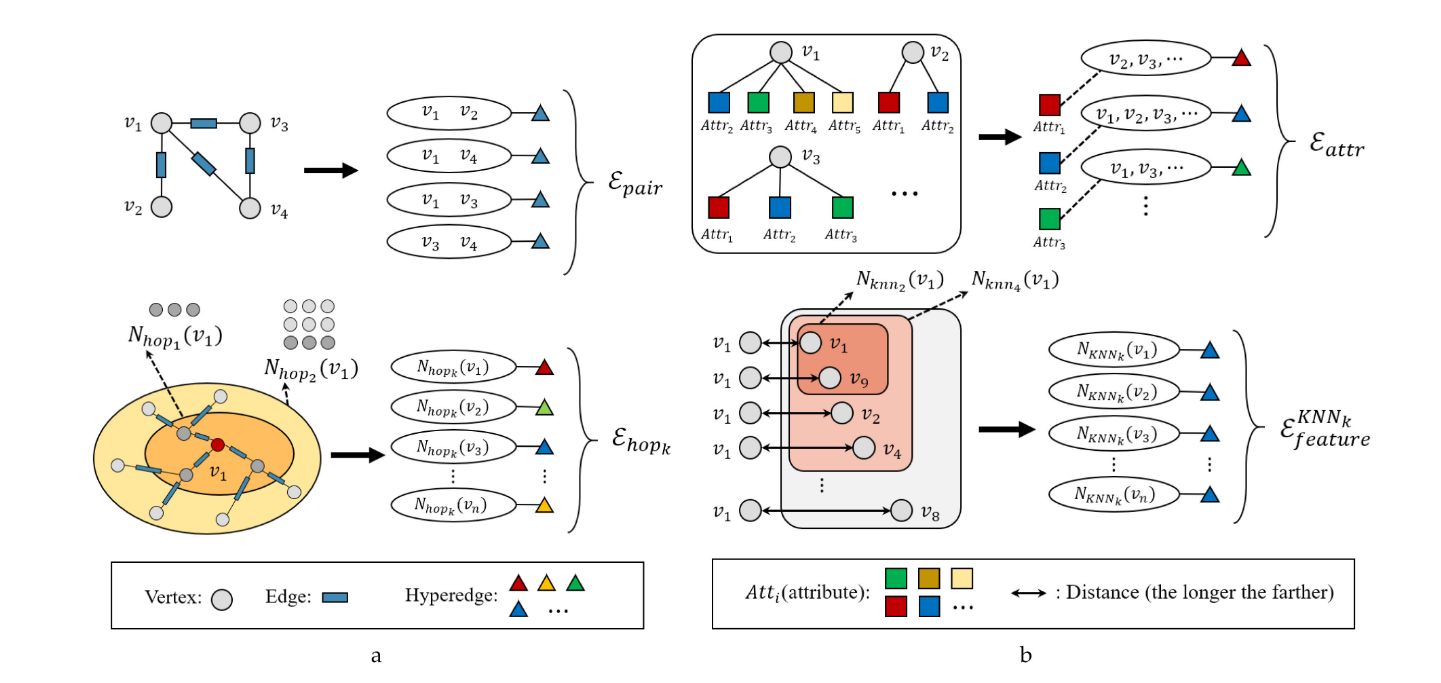
超边生成方法

3.1.1 具有图结构的数据

对于已经具有图结构的数据Gs=(Vs,Es)\mathcal{G}_s=\left(\mathcal{V}_s, \mathcal{E}_s\right)，其中vi∈Vsv_i \in \mathcal{V}_s是一个顶点，esij∈Ese_{s_{i j}} \in \mathcal{E}_s是图中连接viv_i和vjv_j的边。令AA表示Gs\mathcal{G}_s的邻接矩阵。给定这样的图结构，可以生成两种类型的超边组如下：

  1. 使用成对边生成超边组Epair\mathcal{E}_{\text{pair}}：将已有图结构中的每条边视为一个 2 元超边，其中该组中的每个超边eije_{ij}只连接图Gs\mathcal{G}_s中对应边的两个顶点viv_i和vjv_j​：

    Epair={{vi,vj}∣(vi,vj)∈Es}\mathcal{E}_{\text{pair}}=\left\{\left\{v_i, v_j\right\} \mid\left(v_i, v_j\right) \in \mathcal{E}_s\right\}

    • Epair\mathcal{E}_{\text{pair}}能够完全覆盖图结构中的低阶（成对）相关性，这是高阶相关性建模所需的基本信息。

  2. 使用k-Hop邻居生成超边组Ehop\mathcal{E}_{\text{hop}}：将某节点的 k-hop 邻居组成一个超边，建模更远距离的关联

    Ehopk={Nhopk(v)∣v∈V}\mathcal{E}_{\text{hop}_k}=\left\{N_{\text{hop}_k}(v) \mid v \in \mathcal{V}\right\}

    • Ehop\mathcal{E}_{\text{hop}}通过扩展图结构中的搜索半径，能够为中心顶点找到外部相关顶点，从而生成顶点组而不仅仅是两个顶点的超边。相比于Epair\mathcal{E}_{\text{pair}}中的成对关联，它可以提供更丰富的关联信息

3.1.2 没有图结构的数据

对于没有图结构的数据可以使用属性attribute或特征feature生成超边组：

  1. 使用属性生成超边组Eattribute\mathcal{E}_{\text{attribute}}：把同一属性的所有元素用一条超边连起来，一条超边表示一种属性

    Efeat={Natt(a)∣a∈A}\mathcal{E}_{\text{feat}}=\left\{N_{att}(a) | a \in A\right\}

    • Eattribute\mathcal{E}_{\text{attribute}}可以从组级别对属性空间中的相关性进行建模。

  2. 使用特征生成超边组Efeature\mathcal{E}_{\text{feature}}：利用特征空间中的 KNN 或半径范围聚类来构造超边

    {EfeatureKNNk={NKNNk(v)∣v∈V}Efeaturedistanced={Ndisd(v)∣v∈V}​\left\{ \begin{array}{l} \mathcal{E}_{\text{feature}}^{\mathrm{KNN}_k}=\left\{N_{\mathrm{KNN}_k}(v) \mid v \in \mathcal{V}\right\} \\ \mathcal{E}_{\text{feature}}^{\text{distance}_d}=\left\{N_{\text{dis}_d}(v) \mid v \in \mathcal{V}\right\} \end{array} \right.​

    • Efeature\mathcal{E}_{\text{feature}}旨在找到顶点特征背后的关系。它可以在多个尺度上设置，例如在邻居查找过程中设置不同的kk或dd值。

3.2 超边组融合

在使用上述策略生成多个超边组之后，无论这些超边组是通过策略生成的还是天然存在的，我们都需要将它们进一步组合以生成最终的超图。这相当于是多模态数据的融合：每种生成的超边的方法都会生成一个超边组，每个组相当于是一种模态，我们需要联合处理所有模态的数据，所以要进行多模态数据融合，即超边组融合。

假设有KK个超边组{E1,E2,⋯ ,EK}\left\{\mathcal{E}_1, \mathcal{E}_2, \cdots, \mathcal{E}_K\right\}，我们可以分别得到KK个关联矩阵Hk∈{0,1}N×Mk\mathbf{H}_k \in \{0,1\}^{N \times M_k}。

3.2.1 等权融合(Coequal Fusion)

构建超图G\mathcal{G}的最简单的融合方式是直接将所有超边组的关联矩阵拼接起来，超图的超边权重矩阵可以赋值为 1，以便平等对待每个超边

\mathbf{H}=\mathbf{H}_1 \| \mathbf{H}_2 \| \cdots \| \mathbf{H}_K$$​ 其中$\|$是矩阵拼接操作concat #### 3.2.2 自适应融合(Adaptive Fusion) 考虑到不同超边组的信息丰富度差异很大，简单的等权融合无法充分利用多模态混合的高阶关联。因此，本文提出了一种超边组融合的自适应策略，即自适应融合（Adaptive Fusion）。具体来说，每个超边组都关联一个可训练参数，该参数可以自适应地调整多个超边组对最终顶点嵌入的影响 $$\left\{ \begin{array}{l} \mathbf{w}_k=\operatorname{copy}\left(\operatorname{sigmoid}\left(w_k\right), M_k\right) \\ \mathbf{W}=\operatorname{diag}\left(\mathbf{w}_1^1, \cdots, \mathbf{w}_1^{M_1}, \cdots, \mathbf{w}_K^1, \cdots, \mathbf{w}_K^{M_K}\right), \\ \mathbf{H}=\mathbf{H}_1 \| \mathbf{H}_2 \| \cdots \| \mathbf{H}_K \end{array} \right.

其中:

  • sigmoid⁡(⋅)\operatorname{sigmoid}(\cdot)是逐元素归一化函数

  • copy⁡(a,b)\operatorname{copy}(a, b)函数返回一个大小为bb的向量，该向量的值通过复制aa共bb次填充

  • M=M1+M2+⋯+MKM=M_1+M_2+\cdots+M_K表示所有超边组中超边的总和

  • wk∈R\mathbf{w}_k \in \mathbb{R}是一个由超边组kk内部所有超边共享的可训练参数，向量wk=(wk1,⋯ ,wkMk)∈RMk\mathbf{w}_k = \left(\mathbf{w}_k^1, \cdots, \mathbf{w}_k^{M_k}\right) \in \mathbb{R}^{M_k}表示生成的超边组kk的权重向量。

  • W∈RM×M\mathbf{W} \in \mathbb{R}^{M \times M}是一个对角矩阵，表示超图的权重矩阵，其中每个元素Wii\mathbf{W}^{ii}表示对应超边eie_i的权重

  • H∈{0,1}N×M\mathbf{H} \in \{0,1\}^{N \times M}表示通过拼接多个超边组的关联矩阵生成的超图的关联矩阵

四、超图卷积

4.1 超图上的谱卷积

超图谱卷积是基于超图拉普拉斯算子（Hypergraph Laplacian Operator）来进行卷积操作的。HGNN+使用了归一化的超图拉普拉斯算子L=I−D−1/2HWHTD−1/2\mathbf{L}=\mathbf{I}-\mathbf{D}^{-1 / 2} \mathbf{H} \mathbf{W} \mathbf{H}^T \mathbf{D}^{-1 / 2}，其中I\mathbf{I}是单位矩阵，D\mathbf{D}是度矩阵，H\mathbf{H}是超边组的关联矩阵，W\mathbf{W}是超边组的权重矩阵。

当我们有第tt层的超图信号$X_t4时，我们的超边卷积层HGNNConv可以用下式表示：

Xt+1=σ(Dv−1/2HWDe−1H⊤Dv−1/2XtΘ)\mathbf{X}^{t+1} = \sigma(\mathbf{D}_v^{-1/2}\mathbf{HW}\mathbf{D}_e^{-1}\mathbf{H}^{\top}\mathbf{D}_v^{-1/2}\mathbf{X}^t\boldsymbol{\Theta})

其中：

  • Dv\mathbf{D}_v是顶点度矩阵，De\mathbf{D}_e是超边度矩阵
  • W\mathbf{W}是超边组的权重矩阵
  • H\mathbf{H}是超边组的关联矩阵
  • Θ\boldsymbol{\Theta}是在训练过程中要学习的参数

4.2 超图上的空间卷积

4.2.1 超路径

在超图中，我们定义的“路径”称为超路径（hyperpath），它在两个不同的顶点v1v_1和vkv_k之间是一系列的顶点和超边的序列：

P(v1,vk)=(v1,e1,v2,e2,…,vk−1,ek,vk)P(v_1, v_k) = (v_1, e_1, v_2, e_2, \ldots, v_{k-1}, e_k, v_k)

其中，vjv_j和vj+1v_{j+1}属于同一超边eje_j指定的顶点子集。显然，超路径中相邻的两个顶点由一个超边分隔。消息在超图中的传播通过相关的超边进行，这利用了超边中包含的高阶关系。

4.2.2 邻居关系

定义1：互邻关系（Inter-Neighbor Relation）

定义：在一个超图 G=(V,E,W)G = (V, E, W) 中，节点与其所属超边之间的关系定义为：

N={(v,e)∣H(v,e)=1, v∈V, e∈E}\mathcal{N} = \{ (v, e) \mid H(v, e) = 1,\ v \in V,\ e \in E \}

  • HH 是超图的关联矩阵（incidence matrix）；
  • H(v,e)=1H(v, e) = 1 表示节点 vv 属于超边 ee。

作用：
这个定义建立了节点和超边之间的基础连接关系，为后续的邻居集合和消息传递打下基础。

定义2：超边的节点互邻集（Vertex Inter-Neighbor Set of Hyperedge）

定义：对于超边 e∈Ee \in E，其互邻节点集合定义为：

Nv(e)={v∈V∣(v,e)∈N}\mathcal{N}_v(e) = \{ v \in V \mid (v, e) \in \mathcal{N} \}

作用：
这一集合表示所有属于超边 ee 的节点，是从超边向外看有哪些节点连接它。用于第一阶段消息聚合：从节点收集信息生成超边特征。

定义3：节点的超边互邻集（Hyperedge Inter-Neighbor Set of Vertex）

定义： 对于节点 v∈Vv \in V，其互邻超边集合定义为：

Ne(v)={e∈E∣(v,e)∈N}\mathcal{N}_e(v) = \{ e \in E \mid (v, e) \in \mathcal{N} \}

作用：
该集合表示所有包含该节点 vv 的超边，是从节点向外看它连接了哪些超边。用于第二阶段消息聚合：从超边收集信息更新节点特征。

4.2.3 消息传递和聚合

核心思想：两阶段的消息传递结构

在图神经网络中，消息通常在“节点 → 节点”之间传递。而在超图中，一个超边可能连接多个节点，所以消息传递自然要包括：

节点 → 超边 → 节点（Vertex → Hyperedge → Vertex）

HGNNConv⁺ 将超图卷积划分为 两个阶段的消息传递流程，如下所示：

第一阶段：节点 → 超边（聚合节点生成超边特征）

  • 首先，对于每个超边β\beta，从其顶点互邻集Nv(β)\mathcal{N}_v(\beta)中聚合消息。聚合结果mβtm_\beta^t表示为：

mβt=∑α∈Nv(β)Mvt(xαt)(从节点聚合)m_\beta^t = \sum_{\alpha \in \mathcal{N}_v(\beta)} M_v^t(x_\alpha^t) \quad \text{(从节点聚合)}

这里Mvt(⋅)M^t_v(\cdot)：顶点消息函数，用于将顶点特征xαtx_\alpha^t转换为超边消息

  • 使用超边更新函数Uet(⋅)U_e^t(\cdot)更新超边特征yβty_{\beta}^t​，结合超边权重wβw_\beta和中间特征mβtm_{\beta}^t

yβt=Uet(wβ,mβt)(融合节点消息，更新超边)y_\beta^t = U_e^t(w_\beta, m_\beta^t) \quad \text{(融合节点消息，更新超边)}

第二阶段：超边 → 节点（聚合超边生成节点新特征）

  • 然后，对于每个顶点α\alpha，从其超边互邻集Ne(α)\mathcal{N}_e(\alpha)中聚合消息。聚合结果 mαt+1m_\alpha^{t+1}表示为：

mαt+1=∑β∈Ne(α)Met(xαt,yβt)m_\alpha^{t+1} = \sum_{\beta \in \mathcal{N}_e(\alpha)} M_e^t(x_\alpha^t, y_\beta^t)

这里，Met(⋅)M_e^t(\cdot)是超边消息函数，用于将顶点特征xαtx_\alpha^t和超边特征yβty_\beta^t转换为顶点消息。

  • 使用顶点更新函数Uvt(⋅)U_v^t(\cdot)更新顶点特征xαt+1x_{\alpha}^{t+1}​，结合当前顶点特征xαtx_{\alpha}^t和中间特征mαt+1m_{\alpha}^{t+1}

xαt+1=Uvt(xαt,mαt+1)x_\alpha^{t+1} = U_v^t(x_\alpha^t, m_\alpha^{t+1})

综上，在第tt层的空间超图卷积定义为：

{mβt=∑α∈Nv(β)Mvt(xαt)yβt=Uet(wβ,mβt)(Stage 1){mαt+1=∑β∈Ne(α)Met(xαt,yβt)xαt+1=Uvt(xαt,mαt+1)(Stage 2)\left\{ \begin{aligned} m_\beta^t &= \sum_{\alpha \in \mathcal{N}_v(\beta)} M_v^t\left(x_\alpha^t\right) \\ y_\beta^t &= U_e^t\left(w_\beta, m_\beta^t\right) \end{aligned} \right. \quad \text{(Stage 1)}\\ \\ \left\{ \begin{aligned} m_\alpha^{t+1} &= \sum_{\beta \in \mathcal{N}_e(\alpha)} M_e^t\left(x_\alpha^t, y_\beta^t\right) \\ x_\alpha^{t+1} &= U_v^t\left(x_\alpha^t, m_\alpha^{t+1}\right) \end{aligned} \right. \quad \text{(Stage 2)}

其中：

  • xαtx_\alpha^t是顶点α\alpha在第tt层的输入特征向量，xαt+1x_\alpha^{t+1}是更新后的顶点特征
  • mβtm_\beta^t是超边β\beta的消息，wβw_\beta 是与超边β\beta关联的权重
  • mαt+1m_\alpha^{t+1}是顶点α\alpha的消息，yβty_\beta^t是超边β\beta的特征
  • Mvt(⋅)M_v^t(\cdot)是顶点消息函数，Uet(⋅)U_e^t(\cdot)是超边更新函数，Met(⋅)M_e^t(\cdot)是超边消息函数，Uvt(⋅)U_v^t(\cdot)是顶点更新函数。

4.3 示例

当然可以，下面我通过一个简单的例子来说明 HGNN+ 的空间卷积中那几个定义（互邻关系、超边的节点互邻集、节点的超边互邻集） 是如何在实际超图结构中起作用的。

4.3.1 一个小型超图结构

假设我们有以下超图：

  • 节点集合：V={v1,v2,v3,v4}V = \{v_1, v_2, v_3, v_4\}
  • 超边集合：E={e1,e2}E = \{e_1, e_2\}

超边的连接关系如下：

  • 超边 e1e_1 连接 {v1,v2,v3}\{v_1, v_2, v_3\}
  • 超边 e2e_2 连接 {v2,v4}\{v_2, v_4\}

用 incidence matrix HH 表示为：

e₁ e₂
v₁ 1 0
v₂ 1 1
v₃ 1 0
v₄ 0 1

4.3.2 应用定义说明

定义 1：互邻关系 N\mathcal{N}

列出所有 (v,e)(v, e) 使得 H(v,e)=1H(v,e) = 1：

N={(v1,e1),(v2,e1),(v3,e1),(v2,e2),(v4,e2)}\mathcal{N} = \{(v_1, e_1), (v_2, e_1), (v_3, e_1), (v_2, e_2), (v_4, e_2)\}

定义 2：超边的节点互邻集 Nv(e)\mathcal{N}_v(e)

  • Nv(e1)={v1,v2,v3}\mathcal{N}_v(e_1) = \{v_1, v_2, v_3\}
  • Nv(e2)={v2,v4}\mathcal{N}_v(e_2) = \{v_2, v_4\}

表示每条超边连接的所有节点 —— 第一阶段中消息的来源节点集合。

定义 3：节点的超边互邻集 Ne(v)\mathcal{N}_e(v)

  • Ne(v1)={e1}\mathcal{N}_e(v_1) = \{e_1\}
  • Ne(v2)={e1,e2}\mathcal{N}_e(v_2) = \{e_1, e_2\}
  • Ne(v3)={e1}\mathcal{N}_e(v_3) = \{e_1\}
  • Ne(v4)={e2}\mathcal{N}_e(v_4) = \{e_2\}

表示每个节点参与的所有超边 —— 第二阶段中消息的来源超边集合。

4.3.3 模拟消息传递过程

第一阶段：节点 → 超边

  • 对于 e1e_1，聚合 v1,v2,v3v_1, v_2, v_3 的特征
  • 对于 e2e_2，聚合 v2,v4v_2, v_4 的特征

→ 生成 ye1,ye2y_{e_1}, y_{e_2} 超边特征

第二阶段：超边 → 节点

  • v2v_2 会从两个超边 e1,e2e_1, e_2 收到信息（它连接两个超边）
  • v1v_1、v3v_3 只接收来自 e1e_1
  • v4v_4 只接收来自 e2e_2

→ 更新所有节点的新特征 xv(t+1)x_v^{(t+1)}

4.3.4 总结图示（逻辑图）

1
2
3
4
5
6
v1    v2    v3    v4
 |    ||    |     |
 |    ||    |     |
 e1   ||    e2    |
      ||
   (共享 v2)
  • 超边 e1e_1：三元关系
  • 超边 e2e_2：二元关系
  • 节点 v₂ 参与两个高阶关系，聚合信息更复杂

这个例子说明了：

  • HGNN+ 的消息传递是“节点→超边→节点”的闭环；
  • 每个超边聚合连接节点的信息生成中间表示；
  • 每个节点再从其所属的超边聚合信息，完成一次更新。

五、HGNN+卷积层配置

论文中介绍了一个简单的空间超图卷积层（称为 HGNNConv+），通过指定消息更新函数（顶点消息函数 Mvt(⋅)M_v^t(\cdot)、超边更新函数Uet(⋅)U_e^t(\cdot)、超边消息函数Met(⋅)M_e^t(\cdot)和顶点更新函数Uvt(⋅)U_v^t(\cdot)来实现。

消息更新函数的定义
这些函数用于实现超图中的消息传递和特征更新。具体定义如下：

顶点消息函数Mvt(⋅)M_v^t(\cdot)：

Mvt(xαt)=xαt∣Nv(β)∣M_v^t\left(x_\alpha^t\right) = \frac{x_\alpha^t}{\left|\mathcal{N}_v(\beta)\right|}

  • xαtx_\alpha^t是顶点α\alpha在第tt层的特征
  • Nv(β)\mathcal{N}_v(\beta)是与超边β\beta相关联的顶点集合
  • 该函数将顶点特征标准化，以防止特征值过大

超边更新函数Uet(⋅)U_e^t(\cdot)：

Uet(wβ,mβt)=wβ⋅mβtU_e^t\left(w_\beta, m_\beta^t\right) = w_\beta \cdot m_\beta^t

  • wβw_\beta是超边β\beta的权重
  • mβtm_\beta^t是超边β\beta在第tt层的聚合消息
  • 该函数将顶点特征消息加权合并到超边特征中

超边消息函数Met(⋅)M_e^t(\cdot)：

Met(xαt,yβt)=yβt∣Ne(α)∣M_e^t\left(x_\alpha^t, y_\beta^t\right) = \frac{y_\beta^t}{\left|\mathcal{N}_e(\alpha)\right|}

  • yβty_\beta^t是超边β\beta在第tt层的特征
  • Ne(α)\mathcal{N}_e(\alpha)是与顶点α\alpha相关联的超边集合
  • 该函数将超边特征标准化，以便于顶点特征的更新

顶点更新函数Uvt(⋅)U_v^t(\cdot)：

Uvt(xαt,mαt+1)=σ(mαt+1⋅Θt)U_v^t\left(x_\alpha^t, m_\alpha^{t+1}\right) = \sigma\left(m_\alpha^{t+1} \cdot \boldsymbol{\Theta}^t\right)

  • mαt+1m_\alpha^{t+1}是顶点α\alpha在第t+1t+1层的聚合消息
  • Θt\boldsymbol{\Theta}^t是第tt层的可训练参数矩阵
  • σ(⋅)\sigma(\cdot)是非线性激活函数，例如 ReLU
  • 该函数通过线性变换和激活函数更新顶点特征。

矩阵形式的快速前向传播
为了加速在 GPU/CPU 设备上的前向传播，我们将上述操作重写为矩阵形式。具体过程如下：

  1. 超边特征的生成：
  • 输入顶点特征集合为Xt\mathbf{X}^t
  • 根据定义 1 和 2，关联矩阵H⊤\mathbf{H}^{\top}控制了每个顶点特征的超边互邻关系
  • 我们使用关联矩阵H\mathbf{H}和超边度矩阵De\mathbf{D}_e来指导顶点特征的聚合，生成超边特征集合Yt\mathbf{Y}^t：

Yt=WDe−1H⊤Xt\mathbf{Y}^t = \mathbf{W} \mathbf{D}_e^{-1} \mathbf{H}^{\top} \mathbf{X}^t

  1. 顶点特征的更新：
  • 更新后的顶点特征集合Xt+1\mathbf{X}^{t+1}从超边特征集合Yt\mathbf{Y}^t中生成：

Xt+1=σ(Dv−1HYtΘt)\mathbf{X}^{t+1} = \sigma\left(\mathbf{D}_v^{-1} \mathbf{H} \mathbf{Y}^t \boldsymbol{\Theta}^t\right)

  1. 矩阵形式的 HGNNConv+：
  • 结合以上两个步骤，可以将 HGNNConv+的前向传播过程表示为：

Xt+1=σ(Dv−1HWDe−1H⊤XtΘt)\mathbf{X}^{t+1} = \sigma\left(\mathbf{D}_v^{-1} \mathbf{H W} \mathbf{D}_e^{-1} \mathbf{H}^{\top} \mathbf{X}^t \boldsymbol{\Theta}^t\right)