算法学习——回溯

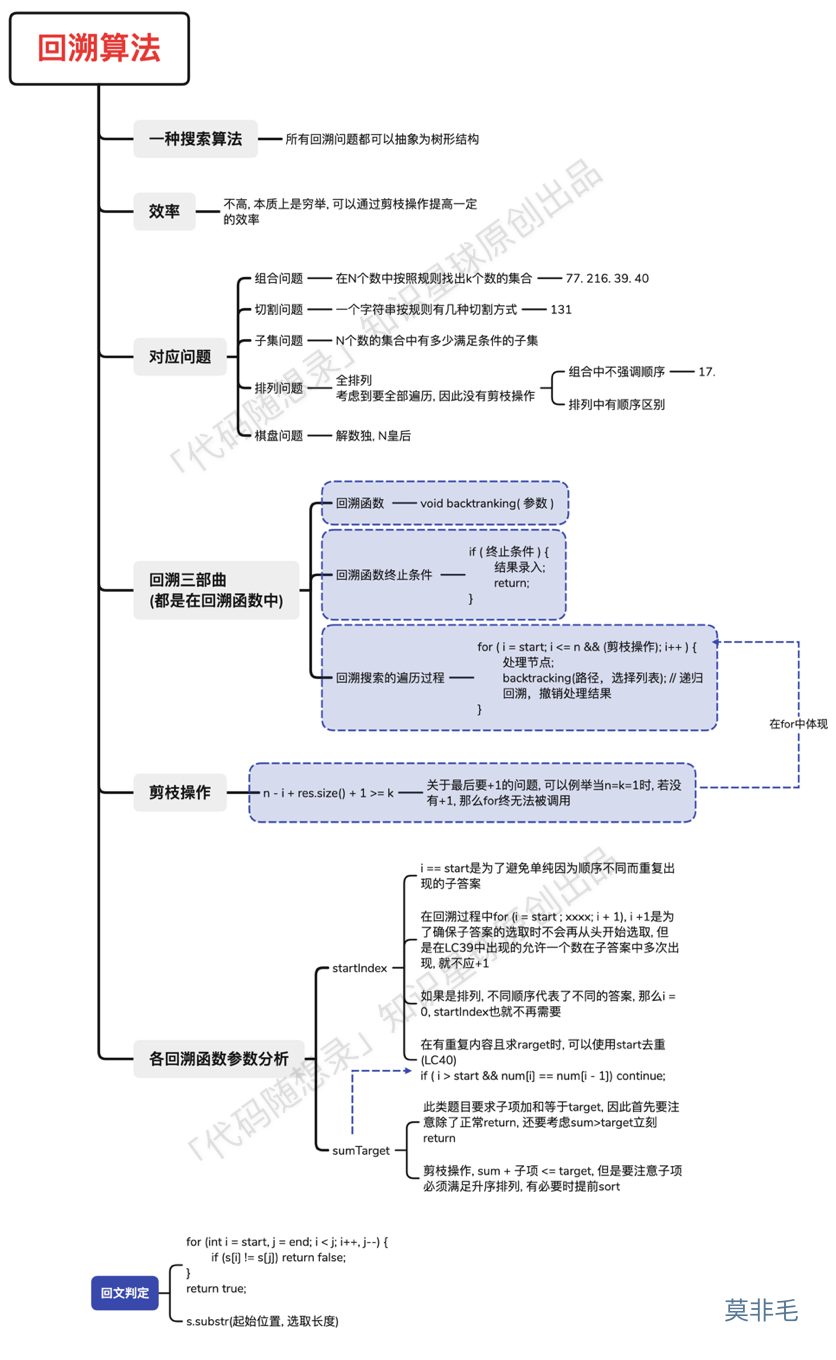
回溯法也可以叫做回溯搜索法，它是一种搜索的方式。

在二叉树系列中，我们已经不止一次，提到了回溯，例如二叉树：以为使用了递归，其实还隐藏着回溯 (opens new window)。

回溯是递归的副产品，只要有递归就会有回溯。

一、回溯法的效率

回溯法的性能如何呢，这里要和大家说清楚了，虽然回溯法很难，很不好理解，但是回溯法并不是什么高效的算法。

因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

那么既然回溯法并不高效为什么还要用它呢？

因为没得选，一些问题能暴力搜出来就不错了，撑死了再剪枝一下，还没有更高效的解法。

此时大家应该好奇了，都什么问题，这么牛逼，只能暴力搜索。

二、回溯法解决的问题

回溯法，一般可以解决如下几种问题：

组合问题：N个数里面按一定规则找出k个数的集合
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
排列问题：N个数按一定规则全排列，有几种排列方式
棋盘问题：N皇后，解数独等等

三、回溯法模板

回溯法的模板如下：

1
2
3
4
5
6
7
8
9
10
11
public void backtrack(参数) {
    if (终止条件) {
        存放结果;
        return;
    }
    for (选择：本层集合中元素(树中节点孩子的数量就是集合的大小)) {
        处理节点;
        backtrack(路径，选择列表);
        回溯，撤销处理结果;
    }
}

四、回溯法中的去重

去重分为树枝去重和树层去重
树枝去重代表在同一个结果中，同一元素不能使用两次
树层去重代表在同一层中，同一元素不能使用两次
比较通用的方法是使用used数组来进行去重
典型例题：Leetcode 47.全排列III

Leetcode 47.全排列III

题目要求

  • 给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：
输入：nums = [1,1,2]
输出：
[[1,1,2],
[1,2,1],
[2,1,1]]

示例 2：
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

解法
与Leetcode46类似，区别在于这道题不仅需要树枝去重，还需要树层去重
需要注意的是代码

1
2
3
if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
    continue;
}

如果改成used[i - 1] == true也是正确的
这是因为used[i - 1] == true是在树枝上去重，used[i - 1] == false是在树层上去重，树层去重效率更高

used[i-1]==false树层去重
used[i-1]==true树枝去重

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Solution {
    public List<List<Integer>> res = new ArrayList<>();
    public List<Integer> path = new ArrayList<>();
    public List<List<Integer>> permuteUnique(int[] nums) {
        boolean[] used = new boolean[nums.length];
        Arrays.fill(used, false);
        // 对数组进行排序，让相同的元素在一起，方便去重
        Arrays.sort(nums);
        backtrack(nums, used);
        return res;
    }

    public void backtrack(int[] nums, boolean[] used) {
        if (path.size() == nums.length) {
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            // used[i - 1] == true，说明同⼀树⽀nums[i - 1]使⽤过，实现树枝去重
            // used[i - 1] == false，说明used[i-1]是用过后设置为的false，
            // 是回溯过去的，即同⼀树层nums[i - 1]使⽤过，也就实现了树层去重
            if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {
                continue;
            }
            //如果同⼀树⽀nums[i]使⽤过那就直接跳过
            if (used[i] == true) continue;
            used[i] = true;//标记同⼀树⽀nums[i]使⽤过，防止同一树枝重复使用
            path.add(nums[i]);
            backTrack(nums, used);
            path.remove(path.size() - 1);//回溯，说明同⼀树层nums[i]使⽤过，防止下一树层重复
            used[i] = false;//回溯
        }
    }
}

五、总结


图源：代码随想录