Leetcode 654.最大二叉树

题目要求

  • 给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
  1. 创建一个根节点，其值为 nums 中的最大值。
  2. 递归地在最大值 左边 的 子数组前缀上 构建左子树。
  3. 递归地在最大值 右边 的 子数组后缀上 构建右子树。
    返回 nums 构建的 最大二叉树 。

示例 1：

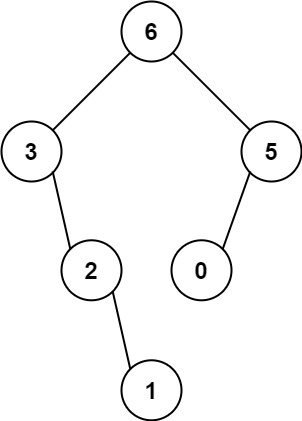
输入：nums = [3,2,1,6,0,5]
输出：[6,3,5,null,2,0,null,null,1]
解释：递归调用如下所示：

  • [3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
    • [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
      • 空数组，无子节点。
      • [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
        • 空数组，无子节点。
        • 只有一个元素，所以子节点是一个值为 1 的节点。
    • [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
      • 只有一个元素，所以子节点是一个值为 0 的节点。
      • 空数组，无子节点。

示例 2：

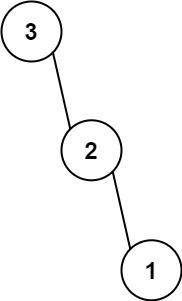
输入：nums = [3,2,1]
输出：[3,null,2,null,1]

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public static TreeNode constructMaximumBinaryTree(int[] nums) {
        if (nums.length == 0) return null;
        return traversal(nums, 0, nums.length - 1);
    }

    // 用于递归添加节点
    public static TreeNode traversal(int[] nums, int start, int end) {
        if (start > end) return null;
        int index = getMax(nums, start, end);
        // 将最大值作为当前节点值
        TreeNode root = new TreeNode(nums[index]);
        // 左子结点为左子数组中的最大值
        root.left = traversal(nums, start, index - 1);
        // 右子结点为右子数组中的最大值
        root.right = traversal(nums, index + 1, end);
        return root;
    }
    
    // 获得数组及子数组中的最大值的index，用于分割数组
    public static int getMax(int[] nums, int start, int end) {
        int max = nums[start];
        int index = start;
        for (int i = start; i <= end; i++) {
            if (nums[i] >= max) {
                max = nums[i];
                index = i;
            }
        }
        return index;
    }
}

代码随想录

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return constructMaximumBinaryTree1(nums, 0, nums.length);
    }

    public TreeNode constructMaximumBinaryTree1(int[] nums, int leftIndex, int rightIndex) {
        if (rightIndex - leftIndex < 1) {// 没有元素了
            return null;
        }
        if (rightIndex - leftIndex == 1) {// 只有一个元素
            return new TreeNode(nums[leftIndex]);
        }
        int maxIndex = leftIndex;// 最大值所在位置
        int maxVal = nums[maxIndex];// 最大值
        for (int i = leftIndex + 1; i < rightIndex; i++) {
            if (nums[i] > maxVal){
                maxVal = nums[i];
                maxIndex = i;
            }
        }
        TreeNode root = new TreeNode(maxVal);
        // 根据maxIndex划分左右子树
        root.left = constructMaximumBinaryTree1(nums, leftIndex, maxIndex);
        root.right = constructMaximumBinaryTree1(nums, maxIndex + 1, rightIndex);
        return root;
    }
}