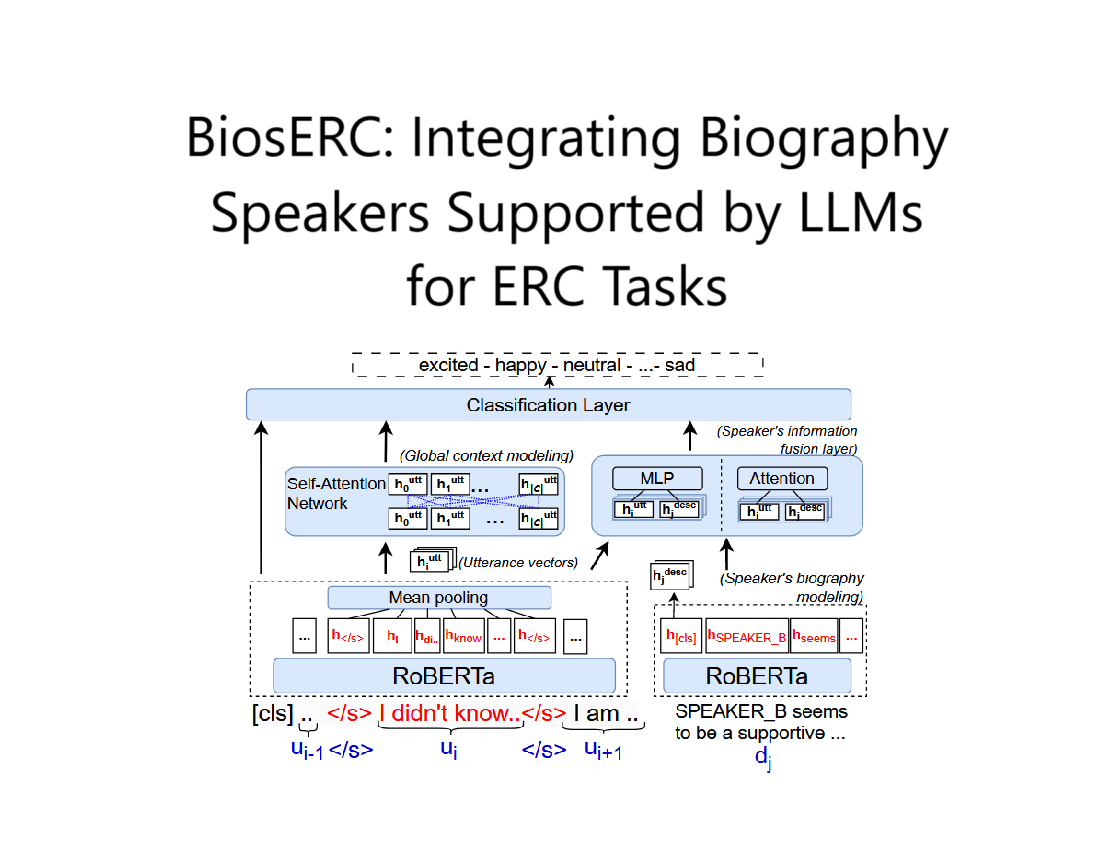
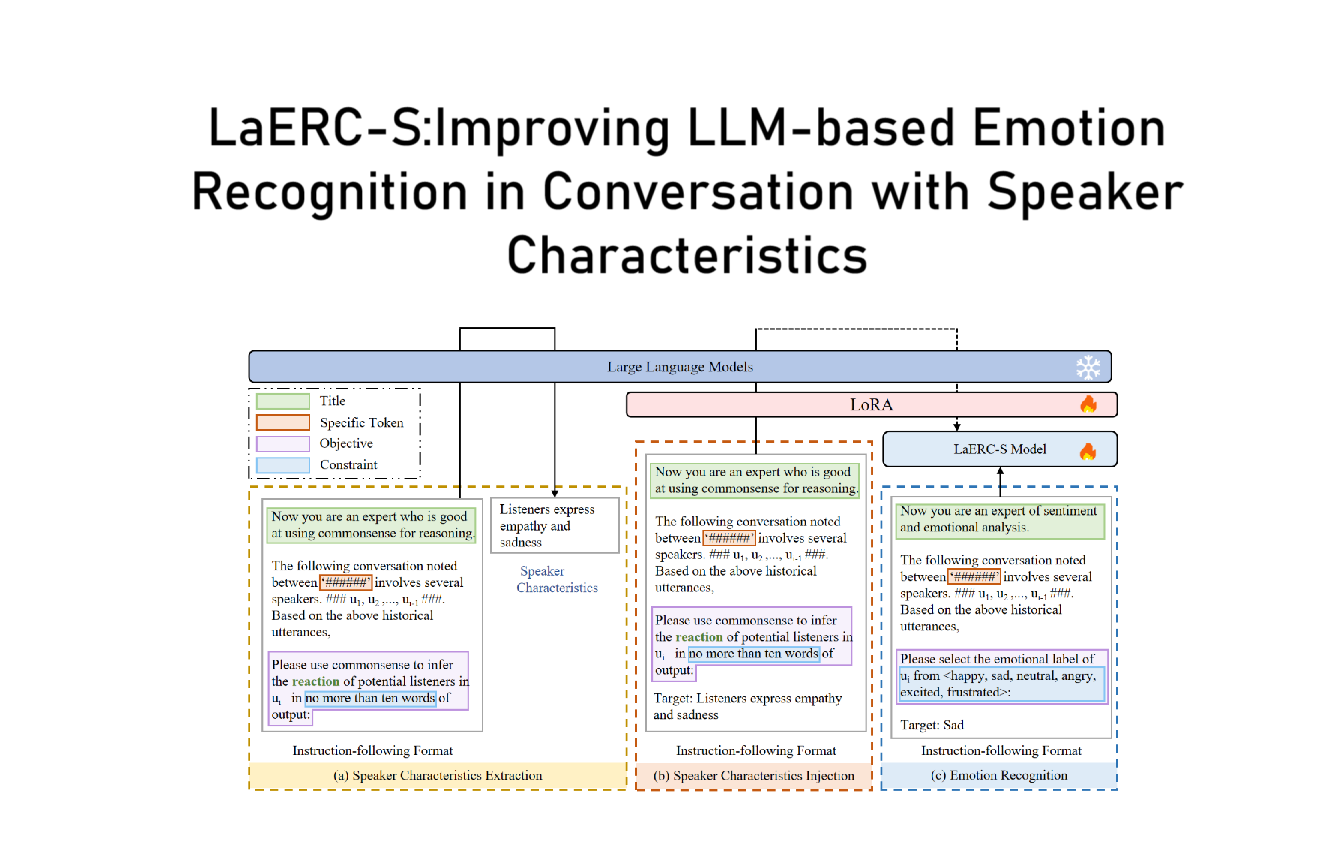
BiosERC:Integrating Biography Speakers Supported by LLMs for ERC Tasks

HyperBERT结构

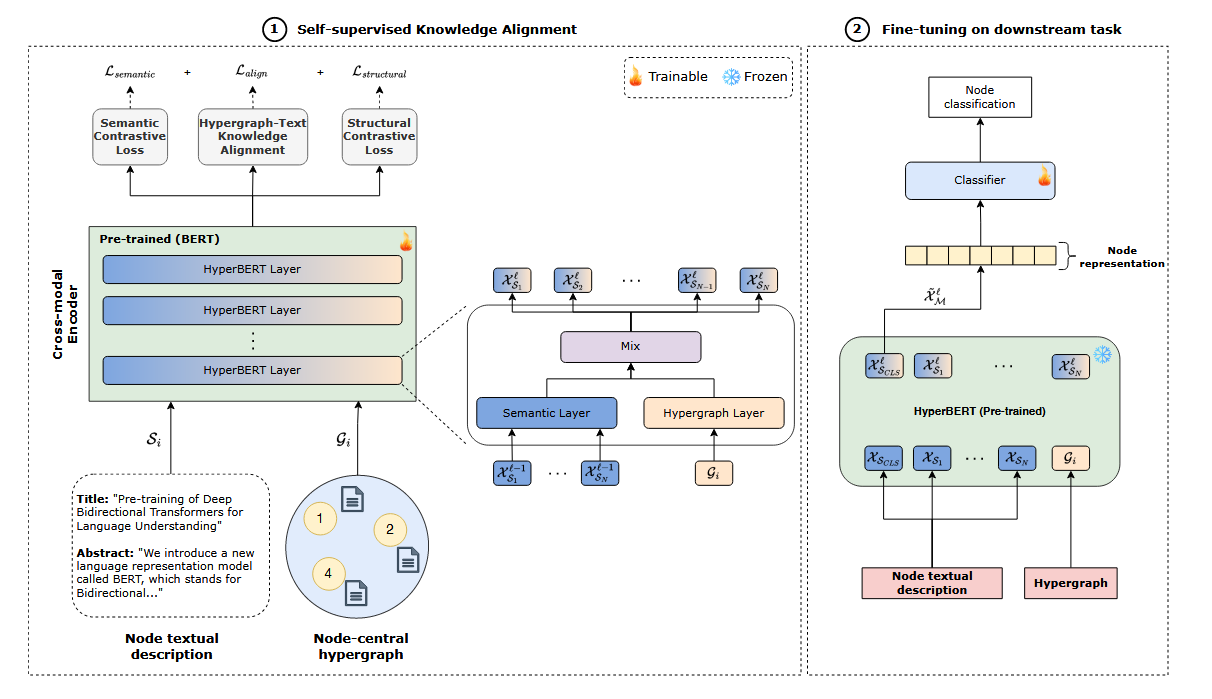
Overview

HyperBERT 单层结构

一个 单层 HyperBERT 主要由两个并行的分支组成：

语义表示层（Semantic Representation Layer）
- 通过 BERT 计算每个超图节点的文本语义表示 $X^\ell_S$ 。
超图结构表示层（Hypergraph Structural Representation Layer）
- 通过 Hypergraph Neural Network (HGNN) 计算超图结构信息 $X^\ell_G$ 。
融合层（Fusion Layer）
- 将文本表示 $X^\ell_S$ 和超图结构表示 $X^\ell_G$ 相加，得到最终的节点表示 $X^\ell_M$ 。

1. 语义表示层（Semantic Representation）

采用 BERT 作为编码器，将超图每个节点的文本属性 $s_i$ 转换为高维向量表示：
$X^\ell_S = \text{BERT}(s_i)$
具体计算流程：
1. 输入：文本 $s_i$ 经过 词嵌入层（Embedding Layer） 转换为向量。
2. 多层 Transformer 计算：
  $X^\ell_S = \text{LayerNorm}(\text{MHA}(X^\ell_S) + X^\ell_S)$
  
  $X^\ell_S = \text{LayerNorm}(\text{FFN}(X^\ell_S) + X^\ell_S)$
3. 最终输出：取 [CLS] 令牌的隐藏状态 作为该节点的文本表示。

2. 超图结构表示层（Hypergraph Structural Representation）

采用 Hypergraph Neural Network (HGNN) 计算超图结构表示：
$X^\ell_G = \sigma (D^{-1} H W B^{-1} H^T X^{(\ell-1)} \Theta)$
其中：
- $ H $ 是超图的关联矩阵（表示节点-超边关系）。
- $ D $ 和 $ B $ 是节点和超边的度矩阵。
- $ W $ 是超边权重。
- $ \Theta $ 是可训练的权重矩阵。
- $ \sigma $ 是非线性激活函数（如 ReLU）。

3. 融合层（Fusion Layer）

通过简单的 加法运算，融合文本信息和超图结构信息：
$X^\ell_M = X^\ell_S + X^\ell_G$
其中：
- $ X^\ell_M $ 是最终的节点表示，包含文本语义 + 超图拓扑结构。

HyperBERT 单层结构总结

单个 HyperBERT 层的完整流程如下：

输入：节点的文本属性 $ s_i $ 和超图结构。
语义表示层：使用 BERT 计算文本嵌入 $ X^\ell_S $。
超图结构表示层：使用 HGNN 计算超图结构表示 $ X^\ell_G $。
融合层：将 $ X^\ell_S $ 和 $ X^\ell_G $ 相加，得到最终的节点表示 $ X^\ell_M $。
输出：$ X^\ell_M $ 作为该层的输出，并传递给下一层或分类任务。

HyperBERT 单层 vs 标准 GNN 层

特性	标准 GNN 层（如 GCN）	HyperBERT 单层
文本处理	不处理文本，仅处理结构	使用 BERT 处理文本
超图结构	使用邻接矩阵	使用超图关联矩阵
信息融合	仅靠结构传播	文本语义 + 结构信息
计算复杂度	低	略高（BERT 计算 + HGNN）

总结

HyperBERT 单层 结合 BERT（文本语义）+ HGNN（超图结构），使模型既能理解文本语义，又能捕捉超图结构。
其核心是 两个分支并行计算，然后相加融合，确保文本和超图信息都能有效地用于节点分类任务。

损失函数

论文中的 损失函数 主要用于 对比学习（contrastive learning），目的是在 文本表示和超图结构表示之间建立一致性，从而更好地利用超图的拓扑信息和文本属性信息。论文定义了三种损失：

语义对比损失（Semantic Contrastive Loss） $ L_{\text{semantic}} $
结构对比损失（Structural Contrastive Loss） $ L_{\text{structural}} $
超图-文本对齐损失（Hypergraph-Text Knowledge Alignment Loss） $ L_{\text{align}} $

最终的 总损失函数 是这些损失的加权和：

$L = \lambda_1 L_{\text{semantic}} + \lambda_2 L_{\text{structural}} + \lambda_3 L_{\text{align}}$

下面详细解析每个损失的作用和计算方式。

1. 语义对比损失（Semantic Contrastive Loss）

目的：让同一超边内的节点在文本语义表示上尽可能相似。

计算方式

$L_{\text{semantic}} = -\frac{1}{|N(i)|} \sum_{p \in N(i)} \log \frac{e^{(X^\ell_S \cdot X^\ell_{Sp} / \tau)}}{\sum_{j \in B(i)} e^{(X^\ell_S \cdot X^\ell_{Sj} / \tau)}}$

参数	含义
$ i $	当前节点
$ p $	当前节点 $ i $ 在超边 $ e $ 内的邻居节点
$ N(i) $	正样本集合：节点 $ i $ 所连接的超边内的其他节点
$ B(i) $	负样本集合：当前 mini-batch 内的其他无关节点
$ X^\ell_S $	文本语义表示：BERT 计算出的当前节点的语义嵌入
$ X^\ell_{Sp} $	正样本的文本表示（BERT 计算）
$ X^\ell_{Sj} $	负样本的文本表示（BERT 计算）
$ \tau $	温度参数，用于控制 softmax 的分布平滑度

解释：

正样本（Positive Samples）：
- 对于一个节点 $ i $，它的同一超边内的节点 $ p \in N(i) $ 作为正样本。
负样本（Negative Samples）：
- 迷你批次（mini-batch）中的其他无关节点 $ j \in B(i) $ 作为负样本。
余弦相似度：
- $ X^\ell_S $ 是 BERT 提取的文本语义表示。
- 计算当前节点的文本表示和其他节点的余弦相似度，然后用 softmax 归一化。
温度参数 $ \tau $：
- 控制分布的平滑程度，较小的 $ \tau $ 会使得模型更倾向于拉近正样本，推远负样本。

作用

让同一超边内的节点在 文本表示空间 内的相似度更高。
通过 softmax 计算 当前节点与正样本的相似度得分，并尽量最大化。
负样本的得分用于对比，确保不同超边的节点之间有较大的差异。

2. 结构对比损失（Structural Contrastive Loss）

目的：让同一超边内的节点在超图结构表示上尽可能相似。

计算方式

$L_{\text{structural}} = -\frac{1}{|N(i)|} \sum_{p \in N(i)} \log \frac{e^{(X^\ell_G \cdot X^\ell_{Gp} / \tau)}}{\sum_{j \in B(i)} e^{(X^\ell_G \cdot X^\ell_{Gj} / \tau)}}$

参数解析

参数	含义
$ i $	当前节点
$ p $	当前节点 $ i $ 在超边 $ e $ 内的邻居节点
$ N(i) $	正样本集合：节点 $ i $ 所连接的超边内的其他节点
$ B(i) $	负样本集合当前 mini-batch 内的其他无关节点
$ X^\ell_G $	超图结构表示：由 HGNN 计算出的当前节点的结构嵌入
$ X^\ell_{Gp} $	正样本的超图结构表示（HGNN 计算）
$ X^\ell_{Gj} $	负样本的超图结构表示（HGNN 计算）
$ \tau $	温度参数，控制 softmax 的分布平滑度

解释：

计算方式与 语义对比损失 相同，但这里使用的是超图结构表示 $X^\ell_G $（由 HGNN 计算得到）。
正样本：
- 仍然是同一超边内的其他节点 $ p \in N(i) $。
负样本：
- 迷你批次中无关的其他节点 $ j \in B(i) $。
目标：
- 让同一超边内的结构表示 $ X^\ell_G $ 也保持一致。

作用

让同一超边内的节点在 超图结构表示空间 内的相似度更高。
确保相连的节点在超图拓扑结构上有相似的表示，同时区分非相连的节点。

3. 超图-文本对齐损失（Hypergraph-Text Knowledge Alignment Loss）

目的：让文本语义表示 $ X^\ell_S $ 和超图结构表示 $ X^\ell_G $ 之间保持一致。

计算方式

$L_{\text{align}} = -\frac{1}{|N(i)|} \sum_{p \in N(i)} \frac{1}{2} \left( L_{\text{align1}} + L_{\text{align2}} \right)$

其中：

$L_{\text{align1}} = \log \frac{e^{(X^\ell_G \cdot X^\ell_{Sp} / \tau)}}{\sum_{j \in B(i)} e^{(X^\ell_G \cdot X^\ell_{Sj} / \tau)}}$

$L_{\text{align2}} = \log \frac{e^{(X^\ell_S \cdot X^\ell_{Gp} / \tau)}}{\sum_{j \in B(i)} e^{(X^\ell_S \cdot X^\ell_{Gj} / \tau)}}$

参数解析

参数	含义
$ i $	当前节点
$ p $	当前节点 $ i $ 在超边 $ e $ 内的邻居节点
$ N(i) $	正样本集合：节点 $ i $ 所连接的超边内的其他节点
$ B(i) $	负样本集合：当前 mini-batch 内的其他无关节点
$ X^\ell_S $	文本语义表示（BERT 计算）
$ X^\ell_G $	超图结构表示（HGNN 计算）
$ X^\ell_{Sp} $	正样本的文本表示（BERT 计算）
$ X^\ell_{Gp} $	正样本的超图结构表示（HGNN 计算）
$ X^\ell_{Sj} $	负样本的文本表示（BERT 计算）
$ X^\ell_{Gj} $	负样本的超图结构表示（HGNN 计算）
$ \tau $	温度参数，控制 softmax 的分布平滑度

解释：

对齐策略：
- $ L_{\text{align1}} $：超图结构表示 $ X^\ell_G $ 作为查询，匹配文本语义表示 $ X^\ell_S $。
- $ L_{\text{align2}} $：文本语义表示 $ X^\ell_S $ 作为查询，匹配超图结构表示 $ X^\ell_G $。
- 两者求平均，确保双向对齐。
目标：
- 让同一节点的文本表示和结构表示互相靠近，从而实现超图结构信息和文本语义信息的融合。

作用

对齐文本表示和超图结构表示，确保两个模态的信息能够互相匹配。
$ L_{\text{align1}} $ 强制 超图结构表示 $ X^\ell_G $ 预测出相似的文本表示 $ X^\ell_S $。
$ L_{\text{align2}} $ 强制 文本表示 $ X^\ell_S $ 预测出相似的超图结构表示 $ X^\ell_G $。
使得 BERT 提取的文本语义和超图结构信息在同一特征空间中更加一致，提高融合效果。

4. 总损失函数

最终的损失函数是三者的加权和：

$L = \lambda_1 L_{\text{semantic}} + \lambda_2 L_{\text{structural}} + \lambda_3 L_{\text{align}}$

参数解析

参数	含义
$ L_{\text{semantic}} $	语义对比损失，使同一超边的文本表示更接近
$ L_{\text{structural}} $	结构对比损失，使同一超边的超图结构表示更接近
$ L_{\text{align}} $	超图-文本对齐损失，让文本和超图表示保持一致
$ \lambda_1, \lambda_2, \lambda_3 $	超参数，控制三种损失的重要性

解释：

$ \lambda_1, \lambda_2, \lambda_3 $ 是超参数，控制三种损失的相对重要性。
论文实验表明 设定 $ \lambda_1 = \lambda_2 = \lambda_3 = 1 $ 效果较好。

总结

损失函数	目标	计算方式	效果
$ L_{\text{semantic}} $ 语义对比损失	让同一超边内的节点文本表示相似	计算 BERT 文本表示之间的相似性，使用对比学习	增强同一超边的语义一致性
$ L_{\text{structural}} $ 结构对比损失	让同一超边内的节点超图结构表示相似	计算超图结构表示之间的相似性，使用对比学习	强化超图的拓扑信息建模
$ L_{\text{align}} $ 超图-文本对齐损失	让文本表示和超图结构表示对齐	计算文本表示与结构表示的相似性，确保两者匹配	结合文本和超图信息，提高整体表达能力