Leetcode 459.重复的子字符串

题目要求

  • 给定一个非空的字符串 s ，检查是否可以通过由它的一个子串重复多次构成。

示例 1：
输入: s = “abab”
输出: true
解释: 可由子串 “ab” 重复两次构成。
示例2：
输入: s = “aba”
输出: false
示例3：
输入: s = “abcabcabcabc”
输出: true
解释: 可由子串 “abc” 重复四次构成。 (或子串 “abcabc” 重复两次构成。)

提交

KMP算法

充分性证明:

如果一个字符串s是由重复子串组成，那么 最长相等前后缀不包含的子串一定是字符串s的最小重复子串。

如果s 是由最小重复子串p组成，即 s = n * p

那么相同前后缀可以是这样：

也可以是这样：

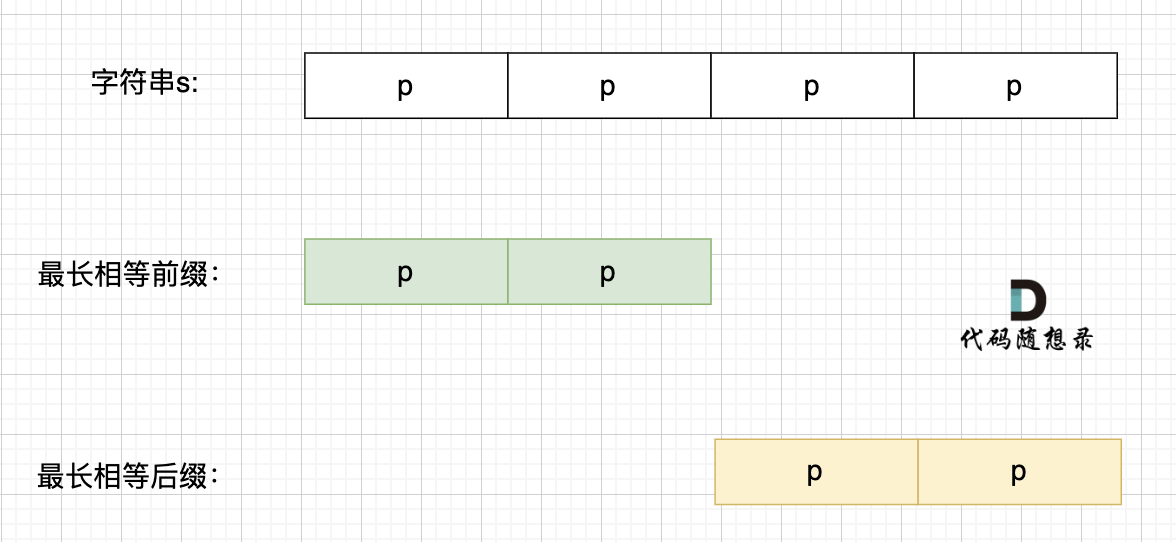
最长的相等前后缀，也就是这样：

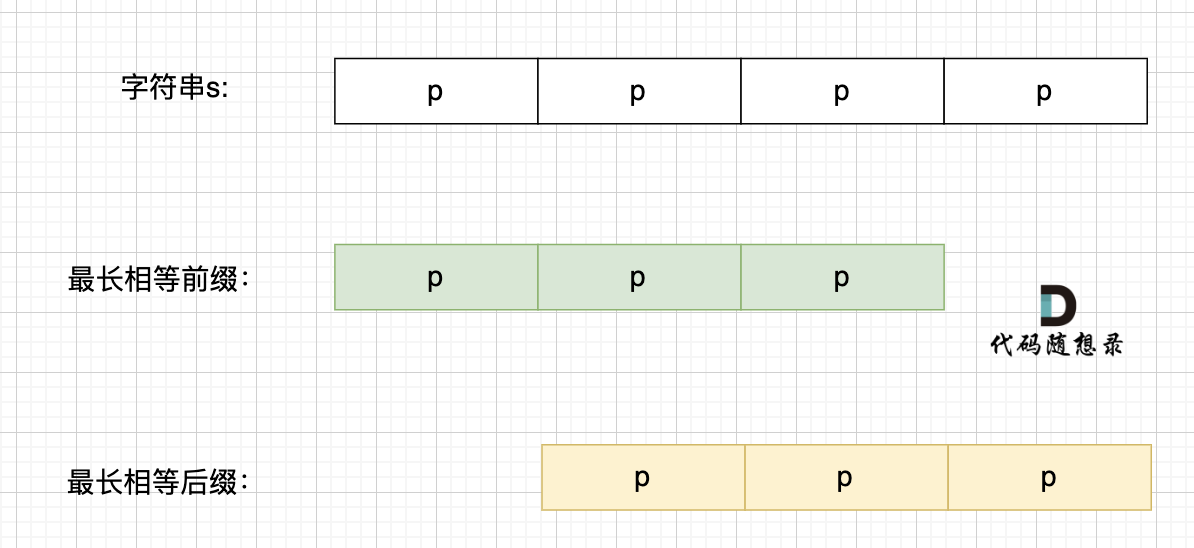
那么有可能是：如果字符串s 是由最小重复子串p组成，最长相等前后缀就不能更长一些？ 例如这样：

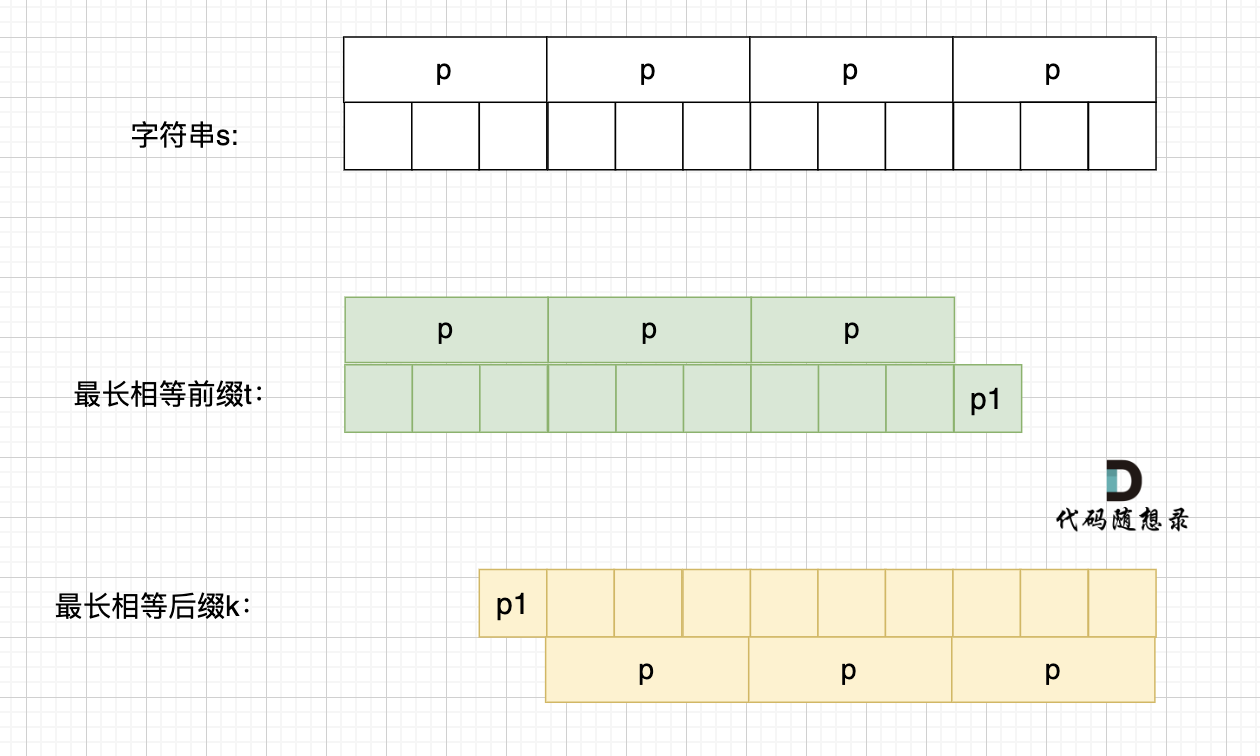
如果这样的话，因为前后缀要相同，所以 p2 = p1，p3 = p2，如图：

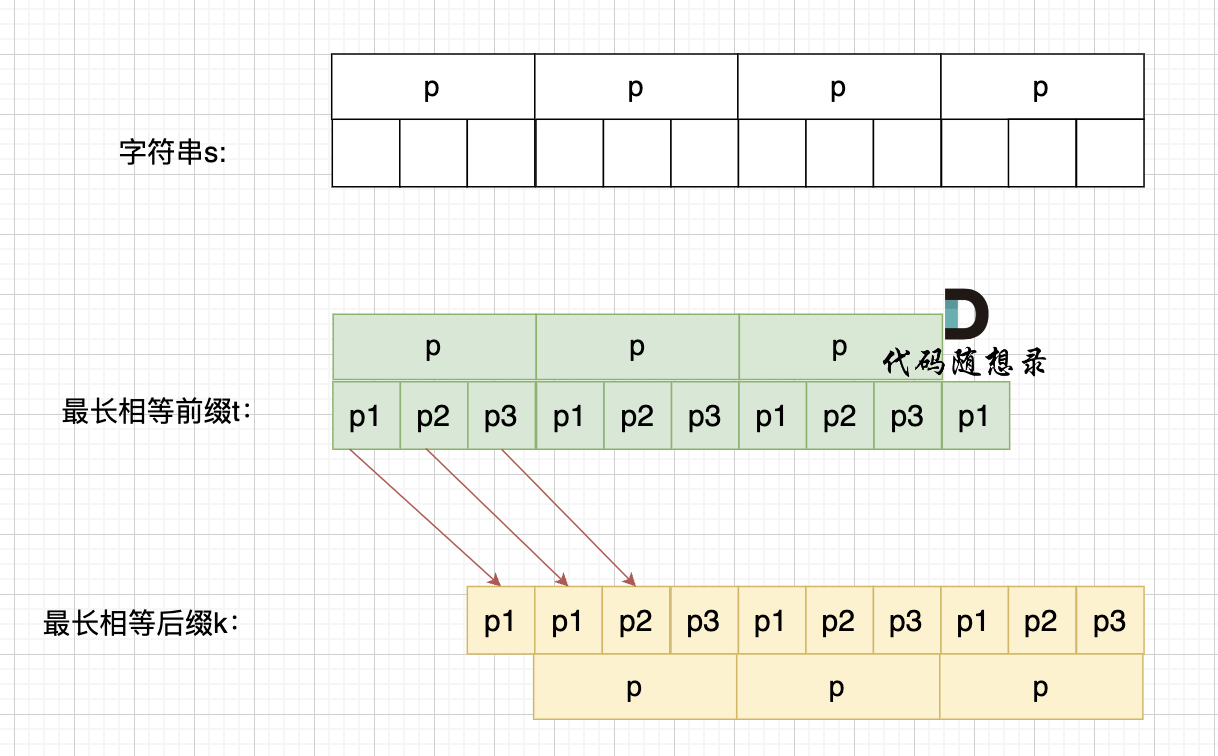
p2 = p1，p3 = p2 即： p1 = p2 = p3

说明 p = p1 * 3。

这样p 就不是最小重复子串了，不符合我们定义的条件。

所以，如果这个字符串s是由重复子串组成，那么最长相等前后缀不包含的子串是字符串s的最小重复子串。

必要性证明

以上是充分性证明，以下是必要性证明：

如果 最长相等前后缀不包含的子串是字符串s的最小重复子串， 那么字符串s一定由重复子串组成吗？

最长相等前后缀不包含的子串已经是字符串s的最小重复子串，那么字符串s一定由重复子串组成，这个不需要证明了。

关键是要证明：最长相等前后缀不包含的子串什么时候才是字符串s的最小重复子串呢。

情况一， 最长相等前后缀不包含的子串的长度 比 字符串s的一半的长度还大，那一定不是字符串s的重复子串，如图：

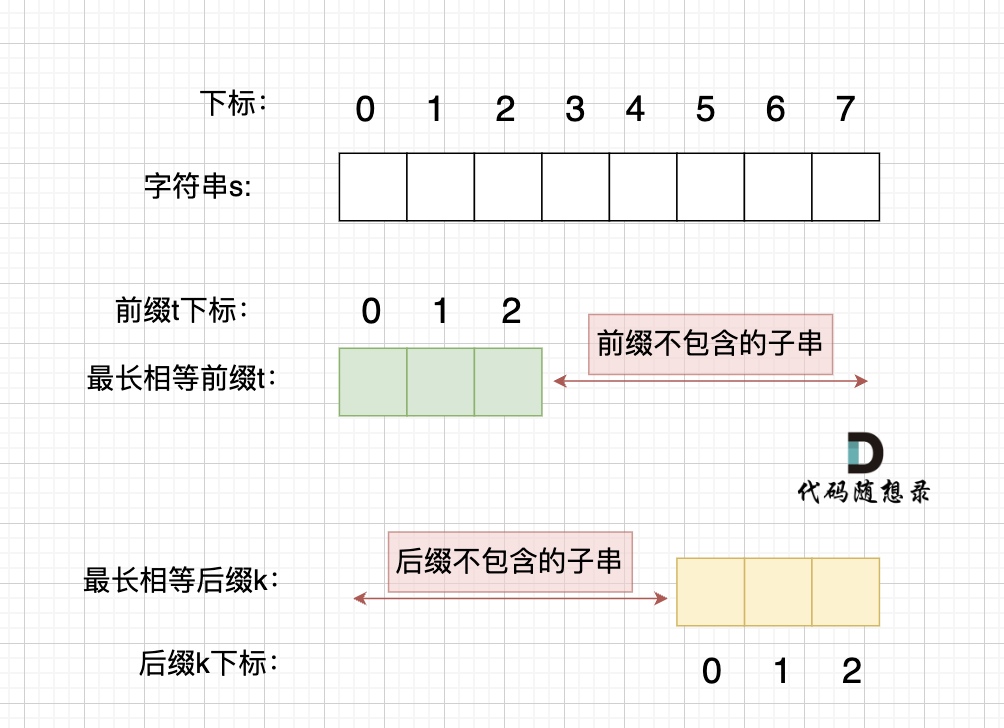
图中：前后缀不包含的子串的长度 大于 字符串s的长度的 二分之一

情况二，最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除，如图：

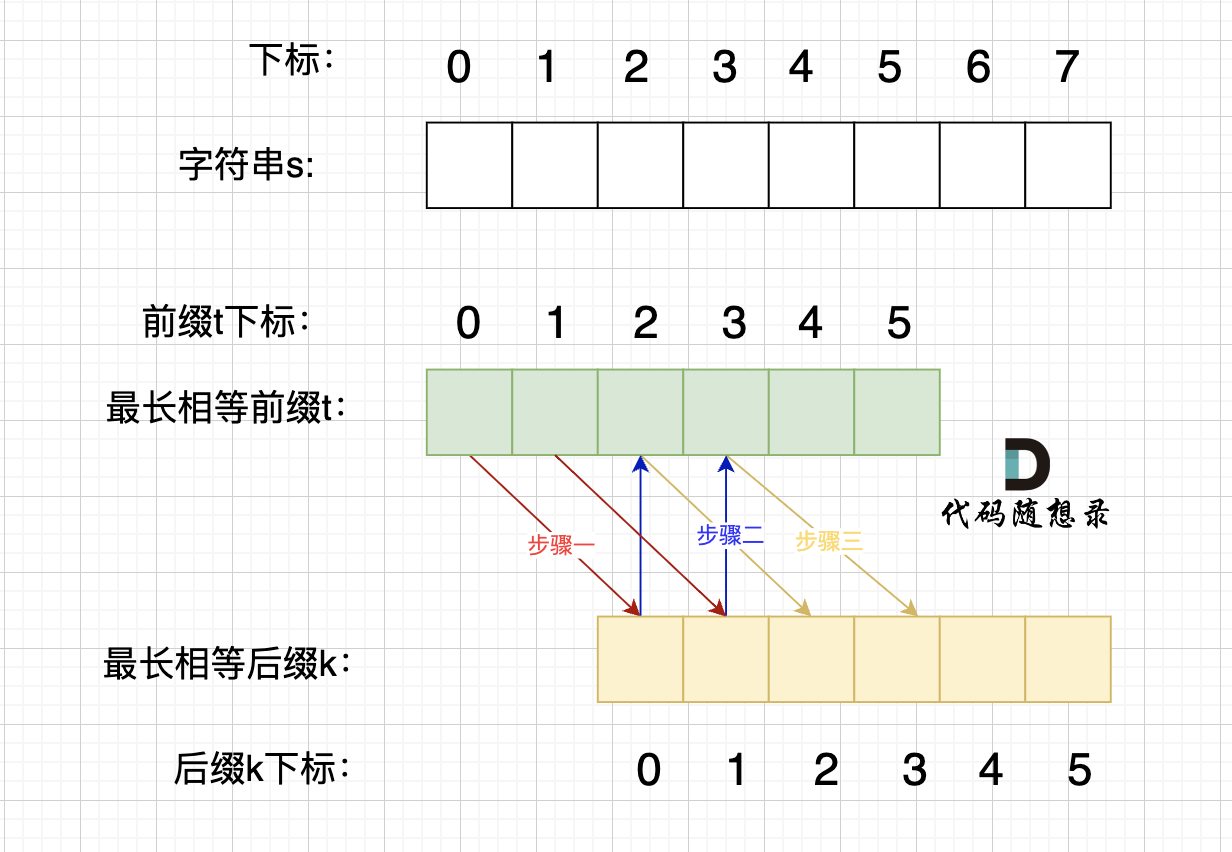
步骤一：因为 这是相等的前缀和后缀，t[0] 与 k[0]相同， t[1] 与 k[1]相同，所以 s[0] 一定和 s[2]相同，s[1] 一定和 s[3]相同，即：，s[0]s[1]与s[2]s[3]相同 。

步骤二： 因为在同一个字符串位置，所以 t[2] 与 k[0]相同，t[3] 与 k[1]相同。

步骤三： 因为 这是相等的前缀和后缀，t[2] 与 k[2]相同 ，t[3]与k[3] 相同，所以，s[2]一定和s[4]相同，s[3]一定和s[5]相同，即：s[2]s[3] 与 s[4]s[5]相同。

步骤四：循环往复。

所以字符串s，s[0]s[1]与s[2]s[3]相同， s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同。

可以推出，在由重复子串组成的字符串中，最长相等前后缀不包含的子串就是最小重复子串。

即 s[0]s[1] 是最小重复子串

以上推导中，录友可能想，你怎么知道 s[0] 和 s[1] 就不相同呢？ s[0] 为什么就不能是最小重复子串。

如果 s[0] 和 s[1] 也相同，同时 s[0]s[1]与s[2]s[3]相同，s[2]s[3] 与 s[4]s[5]相同，s[4]s[5] 与 s[6]s[7] 相同，那么这个字符串就是有一个字符构成的字符串。

那么它的最长相同前后缀，就不是上图中的前后缀，而是这样的的前后缀：

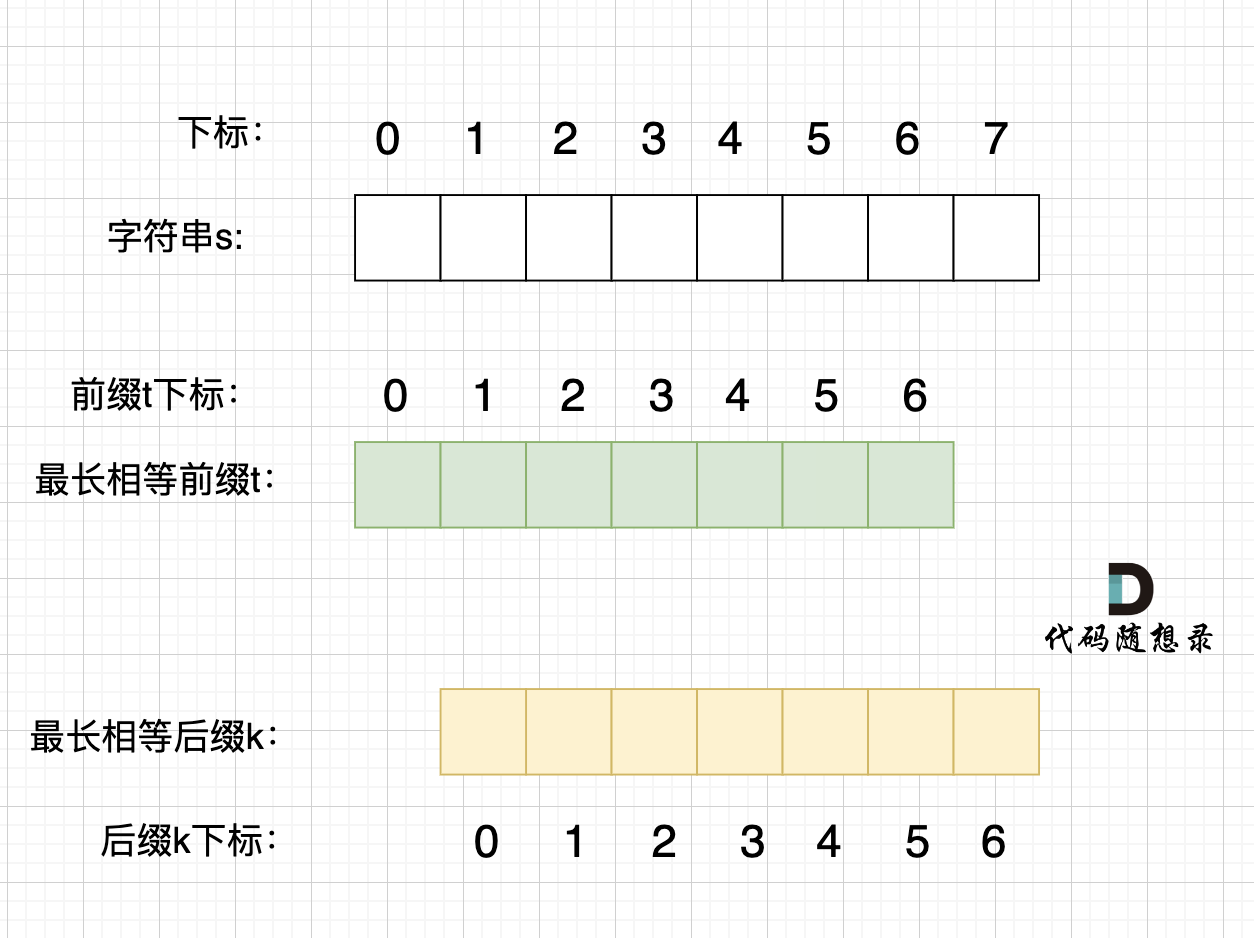
录友可能再问，由一个字符组成的字符串，最长相等前后缀凭什么就是这样的。

自己举个例子，aaaaaa，这个字符串，他的最长相等前后缀是什么？

同上以上推导，最长相等前后缀不包含的子串的长度只要被 字符串s的长度整除，最长相等前后缀不包含的子串一定是最小重复子串。

情况三，最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除得情况，如图：

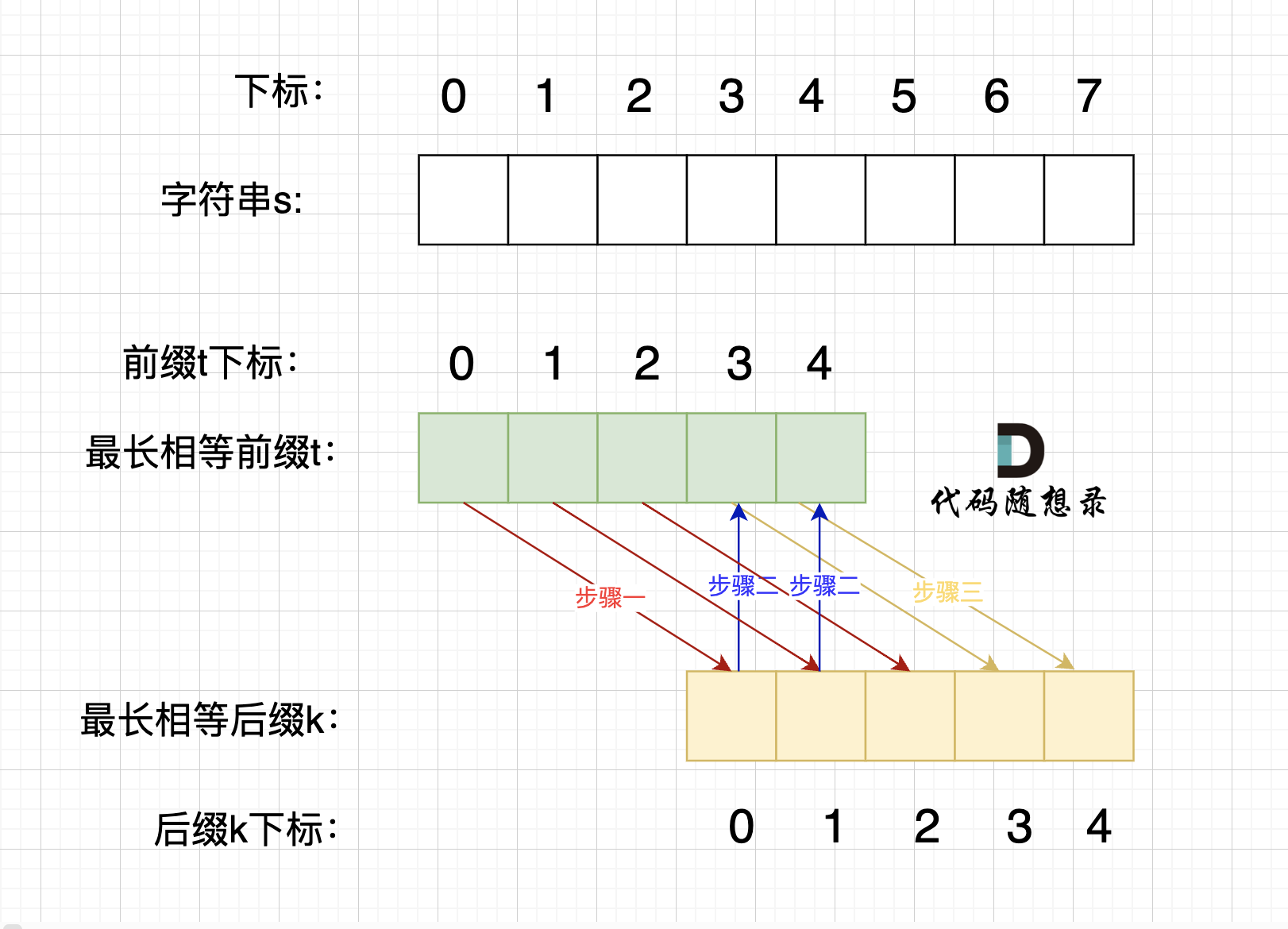
步骤一：因为 这是相等的前缀和后缀，t[0] 与 k[0]相同， t[1] 与 k[1]相同，t[2] 与 k[2]相同。
所以 s[0] 与 s[3]相同，s[1] 与 s[4]相同，s[2] 与s[5]，即：，s[0]s[1]与s[2]s[3]相同 。

步骤二： 因为在同一个字符串位置，所以 t[3] 与 k[0]相同，t[4] 与 k[1]相同。

步骤三： 因为 这是相等的前缀和后缀，t[3] 与 k[3]相同 ，t[4]与k[5] 相同，所以，s[3]一定和s[6]相同，s[4]一定和s[7]相同，即：s[3]s[4] 与 s[6]s[7]相同。

以上推导，可以得出 s[0],s[1],s[2] 与 s[3],s[4],s[5] 相同，s[3]s[4] 与 s[6]s[7]相同。

那么 最长相等前后缀不包含的子串的长度 不被 字符串s的长度整除 ，最长相等前后缀不包含的子串就不是s的重复子串

充分条件：如果字符串s是由重复子串组成，那么 最长相等前后缀不包含的子串 一定是 s的最小重复子串。

必要条件：如果字符串s的最长相等前后缀不包含的子串 是 s最小重复子串，那么 s是由重复子串组成。

在必要条件，这个是 显而易见的，都已经假设 最长相等前后缀不包含的子串 是 s的最小重复子串了，那s必然是重复子串。

关键是需要证明， 字符串s的最长相等前后缀不包含的子串 什么时候才是 s最小重复子串。

同上我们证明了，当 最长相等前后缀不包含的子串的长度 可以被 字符串s的长度整除，那么不包含的子串 就是s的最小重复子串。

代码分析

next 数组记录的就是最长相同前后缀（ 字符串：KMP算法精讲 (opens new window)）， 如果 next[len - 1] != -1，则说明字符串有最长相同的前后缀（就是字符串里的前缀子串和后缀子串相同的最长长度）。

最长相等前后缀的长度为：next[len - 1] + 1。(这里的next数组是以统一减一的方式计算的，因此需要+1，两种计算next数组的具体区别看这里：字符串：KMP算法精讲 (opens new window))

数组长度为：len。

len - (next[len - 1] + 1) 是最长相等前后缀不包含的子串的长度。

如果len % (len - (next[len - 1] + 1)) == 0 ，则说明数组的长度正好可以被 最长相等前后缀不包含的子串的长度 整除 ，说明该字符串有重复的子字符串。

打印数组

强烈建议大家把next数组打印出来，看看next数组里的规律，有助于理解KMP算法

如图：

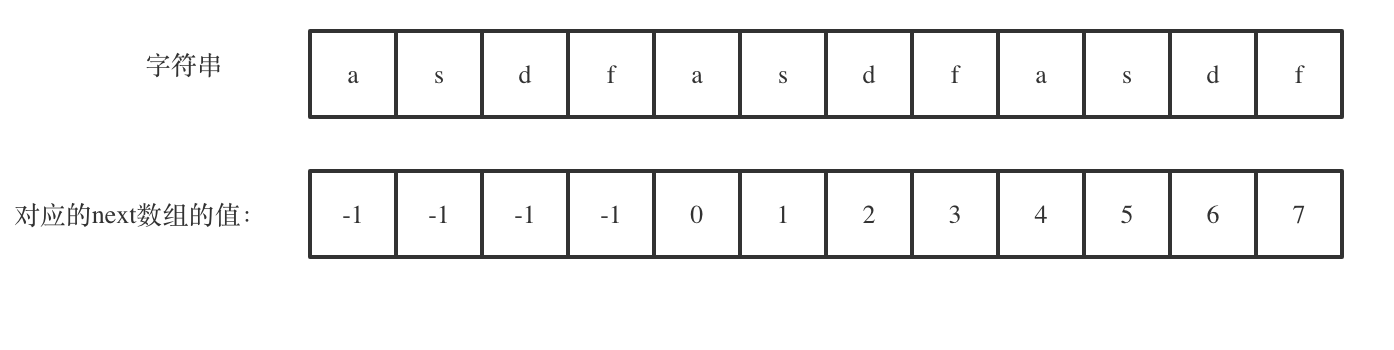
next[len - 1] = 7，next[len - 1] + 1 = 8，8就是此时字符串asdfasdfasdf的最长相同前后缀的长度。

(len - (next[len - 1] + 1)) 也就是： 12(字符串的长度) - 8(最长公共前后缀的长度) = 4， 为最长相同前后缀不包含的子串长度

4可以被 12(字符串的长度) 整除，所以说明有重复的子字符串（asdf）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
    public boolean repeatedSubstringPattern(String s) {
        int n = s.length();

        int[] next = new int[n]; 
        int j = 0;
        next[0] = 0;
        for (int i = 1; i < n; i++) {
            while (j > 0 && s.charAt(i) != s.charAt(j)) // 只要前缀后缀还不一致，就根据前缀表回退j直到起点为止
                j = next[j - 1];
            if (s.charAt(i) == s.charAt(j))
                j++;
            next[i] = j;
        }

        if (next[n - 1] > 0 && n % (n - next[n - 1]) == 0) { 
            return true;
        } else {
            return false;
        }
    }
}

移动匹配

如果您的字符串 S 包含一个重复的子字符串，那么这意味着您可以多次 “移位和换行”`您的字符串，并使其与原始字符串匹配。
例如：abcabc
移位一次：cabcab
移位两次：bcabca
移位三次：abcabc
现在字符串和原字符串匹配了，所以可以得出结论存在重复的子串。
基于这个思想，可以每次移动k个字符，直到匹配移动 length - 1 次。但是这样对于重复字符串很长的字符串，效率会非常低。在 LeetCode 中执行时间超时了。
为了避免这种无用的环绕，可以创建一个新的字符串 str，它等于原来的字符串 S 再加上 S 自身，这样其实就包含了所有移动的字符串。
比如字符串：S = acd，那么 str = S + S = acdacd
acd 移动的可能：dac、cda。其实都包含在了 str 中了。就像一个滑动窗口
一开始 acd (acd) ，移动一次 ac(dac)d，移动两次 a(cda)cd。循环结束
所以可以直接判断 str 中去除首尾元素之后，是否包含自身元素。如果包含。则表明存在重复子串。

1
2
3
4
5
6
class Solution {
   public boolean repeatedSubstringPattern(String s) {
        String str = s + s;
        return str.substring(1, str.length() - 1).contains(s);
}
}