算法学习——KMP算法

KMP算法主要用于解决字符串匹配问题
字符串匹配问题：给定一个文本串"aabaabaaf"，要求判断其中是否含有模式串"aabaaf"，如果有找出其位置

比较经典的暴力解法是使用两层for循环来进行匹配，外层for循环控制从文本串中开始比对的位置，内层for循环控制判断模式串是否匹配
这种方法也叫朴素的模式匹配。这样的做法比较简单，空间复杂度为O(1)，但是时间复杂度为O(mn)，其中mn分别为文本串和模式串的长度

KMP算法所做的优化是，利用已经当前位置之前已经匹配过的位置的信息，创建一个next数组，使得当本次不匹配时可以将下次匹配的起始位置移动到更合适的位置，从而降低时间复杂度

KMP算法中的几个概念：

  • 前缀与后缀： 前缀指包含首字母但不包含尾字母的所有子串；后缀指包含尾字母但不包含首字母的所有子串。
    • 例如对于字符串abcdab，它的前缀集合为：{a,ab,abc,abcd,abcda}，它的后缀集合为：{bcdab,cdab,dab,ab,b}
  • 最长相等前后缀：指的是字符串中最长的相等的前后缀
  • next数组：保存的是模式串中每个子串所对应的最长相等前后缀
    • next数组
  • KMP算法的核心就是在不匹配时指针回退到该位置对应的next数组中所指示的位置，所以KMP算法的关键在于如何求next数组

求解next数组一般有四步：

  1. next数组初始化
  2. 处理前后缀不相同的情况
  3. 处理前后缀相同的情况
  4. 更新next数组

双指针求next数组

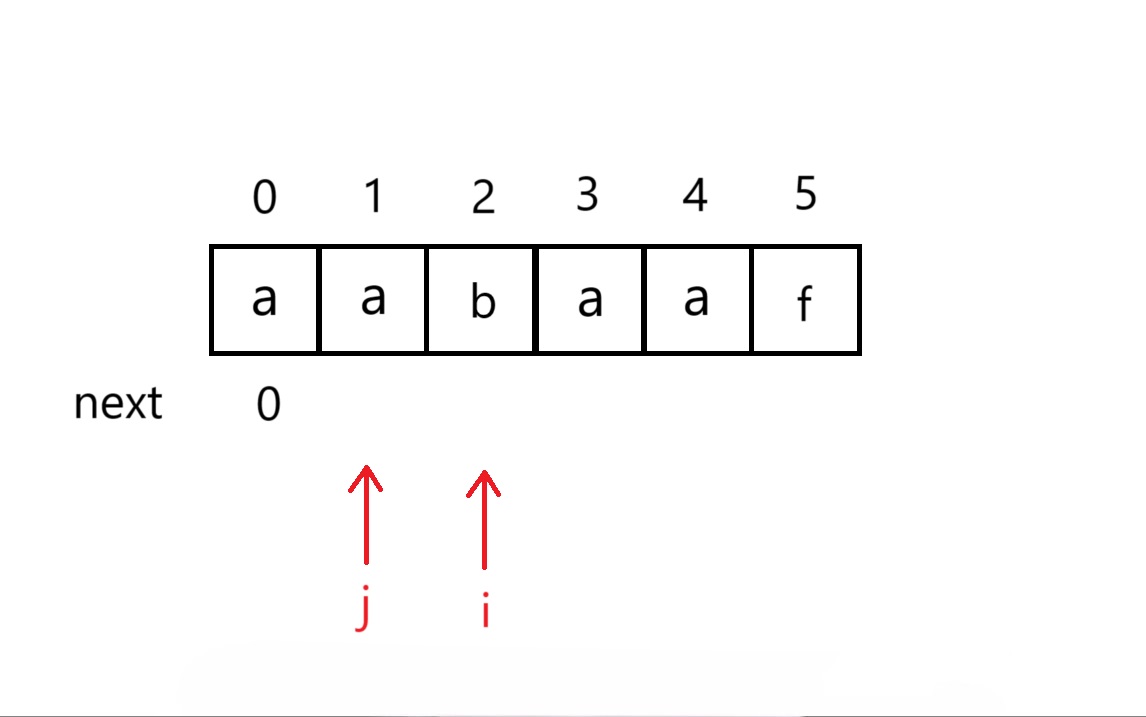
我们会使用到两个指针i和j，其中i表示后缀末尾，j不仅表示前缀末尾，而且表示i包括i之前的子串的最长相等前后缀的长度

我们以模式串"aabaaf"为例来求它的next数组

初始化

首先对于初始化，j代表前缀的末尾，所以j的初始化应该为0，i表示后缀末尾，因为后缀不包含第一个字母，所以i应该初始化为1。next[0]表示如果0位置不匹配应该回退到哪里，因为0已经是第一个位置了，所以next[0]应该初始化为0

1
2
3
4
//next初始化
int j = 0;
int i = 1;
next[0] = 0;

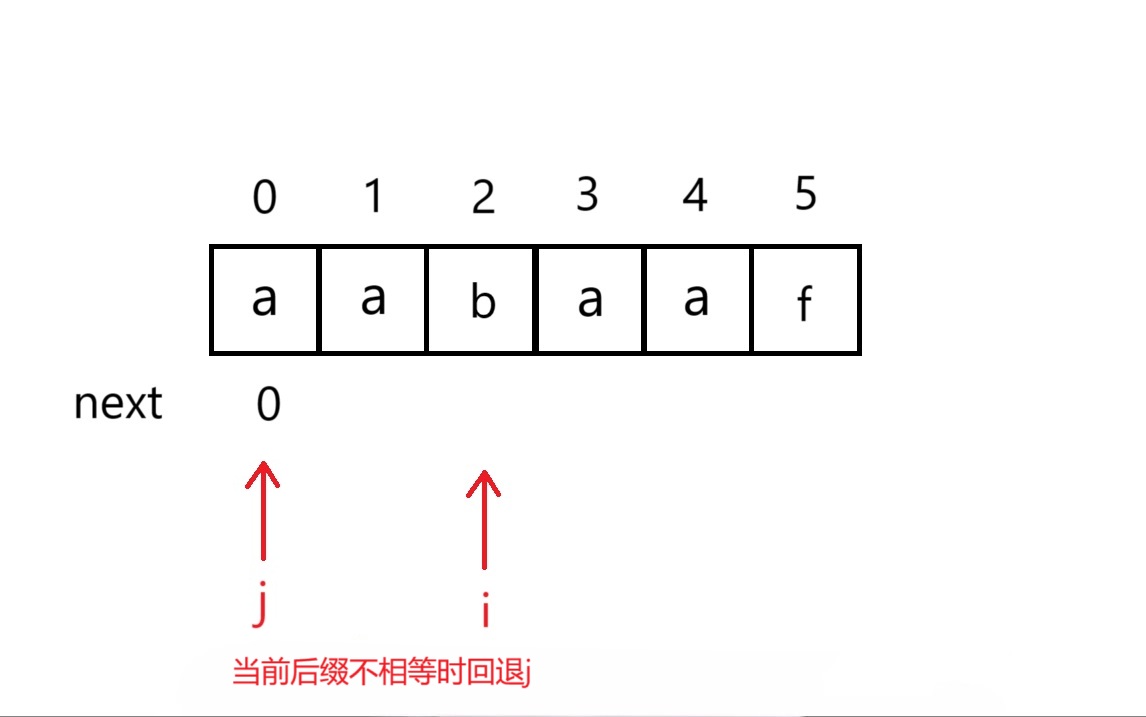
处理前后缀不相等的情况

当我们发现前后缀不相等时，我们需要根据不匹配位置的前一个位置next数组中所存储的位置对j进行回退，直至i、j位置的字符相同
前后缀不相等
回退j

1
2
3
4
5
//回退j
//使用while循环而不是if的原因是当前后缀不相等时我们需要一直回退，而不是只回退一次
while(j > 0 && s[i] != s[j]){
    j = next[j - 1];
}

处理前后缀相等的情况

当前后缀相等时，我们就需要将i和j往后移动，从而判断下一个字母是否相同，如果相同，则说明当前位置是目前最长的相等前后缀，如果不相同，则说明刚才位置是该子串的最长相等前后缀

1
2
3
4
if(s[i] == s[j]){
    j++;
}
//由于i在最外层的for循环中已经i++，所以这里不需要i++了

更新next数组

j代表的不仅仅是前缀末尾，它还代表i包括i之前的子串的最长相等前后缀的长度，所以next[i] = j

1
2
//更新next数组
next[i] = j;

最终求解next数组代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public void getNext(int[] next, String s){
    //初始化
    int j = 0;
    next[0] = 0;
    for(int i = 0; i < s.length(); i++){
        //处理前后缀不相同的情况
        while(j > 0 && s.charAt(j) != s.charAt(i)){
            j = next[j - 1];
        }
        //处理前后缀相同的情况
        if(s.charAt(j) == s.charAt(i)){
            j++;
        }
        //更新next数组
        next[i] = j;
    }    
}