Leetcode 59.螺旋矩阵II
题目要求
- 给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
示例 1:
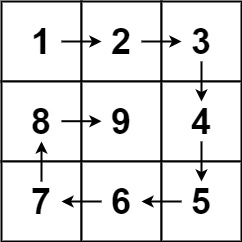
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
示例 2:
输入:n = 1
输出:[[1]]
提交
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
| class Solution {
public int[][] generateMatrix(int n) {
int startx = 0, starty = 0;
int offset = 1;
int count = 1;
int i,j;
int[][] matrix = new int[n][n];
while (startx < n && starty < n) {
for (j = starty; j < n - offset; j++) {
matrix[startx][j] = count++;
}
for (i = startx; i < n - offset; i++) {
matrix[i][j] = count++;
}
for (; j > starty; j--) {
matrix[i][j] = count++;
}
for (; i >startx;i--) {
matrix[i][startx] = count++;
}
startx++;
starty++;
offset++;
}
if(n % 2 != 0){
matrix[n/2][n/2] = count++;
}
return matrix;
}
}
|
官方答案
方法一:模拟
思路及算法:
模拟矩阵的生成。按照要求,初始位置设为矩阵的左上角,初始方向设为向右。若下一步的位置超出矩阵边界,或者是之前访问过的位置,则顺时针旋转,进入下一个方向。如此反复直至填入n^2个元素。
记 matrix 为生成的矩阵,其初始元素设为 0。由于填入的元素均为正数,我们可以判断当前位置的元素值,若不为 0,则说明已经访问过此位置。
复杂度分析:
- 时间复杂度:O(n^2),其中 n 是给定的正整数。矩阵的大小是 n×n,需要填入矩阵中的每个元素。
- 空间复杂度:O(1)。除了返回的矩阵以外,空间复杂度是常数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int[][] generateMatrix(int n) {
int maxNum = n * n;
int curNum = 1;
int[][] matrix = new int[n][n];
int row = 0, column = 0;
int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int directionIndex = 0;
while (curNum <= maxNum) {
matrix[row][column] = curNum;
curNum++;
int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
if (nextRow < 0 || nextRow >= n || nextColumn < 0 || nextColumn >= n || matrix[nextRow][nextColumn] != 0) {
directionIndex = (directionIndex + 1) % 4;
}
row = row + directions[directionIndex][0];
column = column + directions[directionIndex][1];
}
return matrix;
}
}
|
方法二:按层模拟
思路与算法:
可以将矩阵看成若干层,首先填入矩阵最外层的元素,其次填入矩阵次外层的元素,直到填入矩阵最内层的元素。
定义矩阵的第 k 层是到最近边界距离为 k 的所有顶点。例如,下图矩阵最外层元素都是第 1 层,次外层元素都是第 2 层,最内层元素都是第 3 层。
1
2
3
4
5
6
| [[1, 1, 1, 1, 1, 1],
[1, 2, 2, 2, 2, 1],
[1, 2, 3, 3, 2, 1],
[1, 2, 3, 3, 2, 1],
[1, 2, 2, 2, 2, 1],
[1, 1, 1, 1, 1, 1]]
|
对于每层,从左上方开始以顺时针的顺序填入所有元素。假设当前层的左上角位于 (top,left),右下角位于 (bottom,right),按照如下顺序填入当前层的元素。
从左到右填入上侧元素,依次为 (top,left) 到 (top,right)。
从上到下填入右侧元素,依次为 (top+1,right) 到 (bottom,right)。
如果 left<right 且 top<bottom,则从右到左填入下侧元素,依次为 (bottom,right−1) 到 (bottom,left+1),以及从下到上填入左侧元素,依次为 (bottom,left) 到 (top+1,left)。
填完当前层的元素之后,将 left 和 top 分别增加 1,将 right 和 bottom 分别减少 1,进入下一层继续填入元素,直到填完所有元素为止。
复杂度分析:
- 时间复杂度:O(n^2),其中 n 是给定的正整数。矩阵的大小是 n×n,需要填入矩阵中的每个元素。
- 空间复杂度:O(1)。除了返回的矩阵以外,空间复杂度是常数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| class Solution {
public int[][] generateMatrix(int n) {
int num = 1;
int[][] matrix = new int[n][n];
int left = 0, right = n - 1, top = 0, bottom = n - 1;
while (left <= right && top <= bottom) {
for (int column = left; column <= right; column++) {
matrix[top][column] = num;
num++;
}
for (int row = top + 1; row <= bottom; row++) {
matrix[row][right] = num;
num++;
}
if (left < right && top < bottom) {
for (int column = right - 1; column > left; column--) {
matrix[bottom][column] = num;
num++;
}
for (int row = bottom; row > top; row--) {
matrix[row][left] = num;
num++;
}
}
left++;
right--;
top++;
bottom--;
}
return matrix;
}
}
|












