循环神经网络RNN、门控制单元GRU、长短期记忆网络LSTM原理及代码实现

一、循环神经网络（RNN）

循环神经网络（RNN）是用来处理和生成数据序列的模型，广泛应用于自然语言处理、语音识别、时间序列分析等领域。序列模型的关键特性是它能够处理输入和输出之间的依赖关系，使模型能够理解数据在时间或序列上的顺序。
为了建模序列问题，RNN引入了隐状态h(hidden state)的概念，隐状态可以对序列的数据提取特征，接着再转换为输出。通过使用隐藏状态，我们就可以实现对序列数据的处理。
与传统神经网络不同的是，RNN可以支持不定长的输入。传统的神经网络的输入和输出通常都是固定长度的。例如输入图像大小固定，输出是分类结果，没有顺序相关的要求。但RNN可以支持不同长度的输入和输出，适应多种序列任务。

• 一对一（例如图像分类）：一个输入对应一个输出。
• 一对多（例如图像描述生成）：一个输入对应多个输出。
• 多对一（例如情感分析）：多个输入对应一个输出。
• 多对多（例如机器翻译）：多个输入对应多个输出。

1.1 单向循环神经网络

1.1.1 单向RNN结构

单向RNN的结构如图所示：

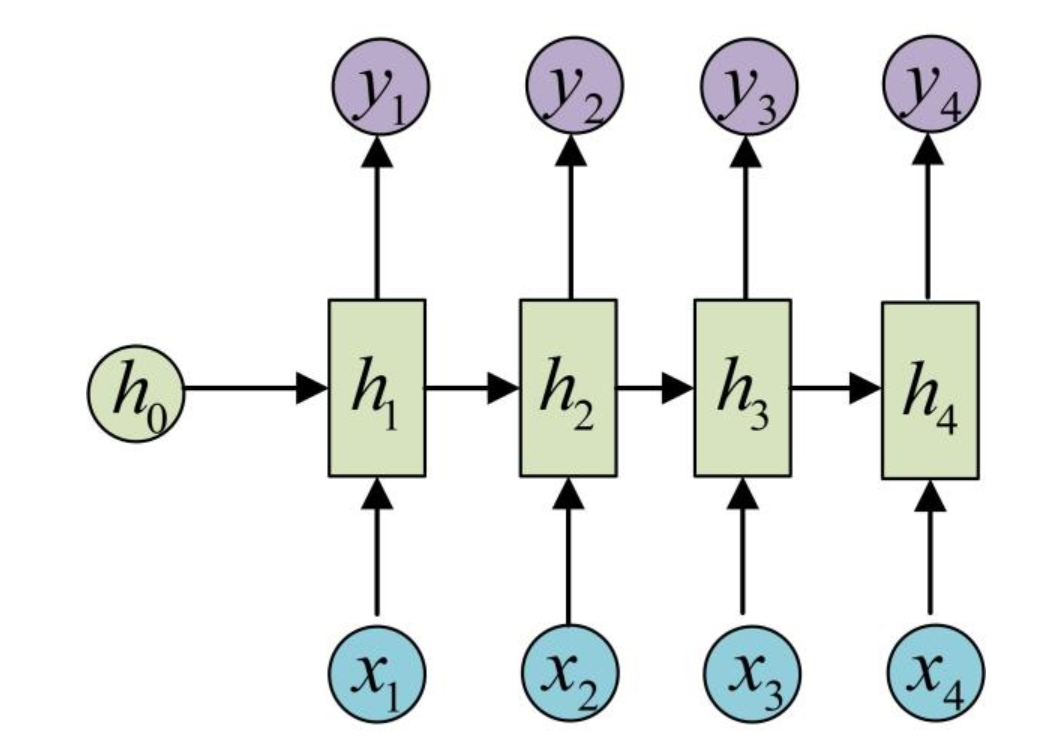
RNN的计算过程如下：

1. 我们初始化一个隐藏状态矩阵$h_0$，然后输入$x_1$。
2. 首先，$h_0$和$x_1$分别经过一个线性层得到$h_1$，然后我们就可以根据$h_1$得到第一个输出$y_1$。
3. 之后我们将$h_1$和$x_2$再分别经过一个线性层计算得到$h_2$，然后我们就可以再根据$h_2$计算得到$y_2$。
4. 以此类推

1.1.2 单向循环网络在Pytorch中的实现

在torch.nn中，RNN的实现原理如下：

$$h_t = tanh(W_{ih}x_t+b_{ih}+W_{hh}h_{t-1}+b_{hh})$$

其中：

• $h_t$是时间t时刻的隐藏状态。
• $x_t$是时间t时刻的输入。
• $h_{t-1}$是时间t-1时刻的隐藏状态。
• $W_{ih}$和$W_{hh}$分别是输入$x_t$和隐藏状态$h_{t-1}$的权重矩阵。
• $b_{ih}$和$b_{hh}$分别是输入$x_t$和隐藏状态$h_{t-1}$的偏置值。
• $tanh()$是非线性激活函数，可以用$ReLu$代替。

RNN的参数有:

• input_size：输入$x$的特征数量。
• hidden_size：隐藏层$h$的特征数量。
• num_layers：RNN层的数量，num_layers=2表示用两个RNN层形成一个多层RNN，第二个RNN层的输入是第一个RNN层的输出。默认为1。
• nonlinearity：非线性函数，可以是“tanh”或“ReLu”。默认为“tanh”。
• bias：是否使用偏置值。默认为True。
• batch_first：决定输入和输出的格式。如果为True，那么我们的输入和输出张量的格式就是(batch,seq,feature)，如果为False，那么我们的输入和输出张量的格式就是(seq,batch,feature)。默认为False。
• dropout：dropout参数。默认为0。
• bidirectional：是否为双向RNN。如果为True则表示使用双向RNN。如果是双向RNN，那么输出就是两倍的hidden_size。默认为False。

RNN的输入：

• input：当batch_first=False时输入形状为($L$,$N$,$H_{in}$)，当batch_first=True时输入形状为($N$,$L$,$H_{in}$)。
• h_0：形状为($D*num_layers$,$N$,$H_{out}$)。
  其中：
• $N$ = batch size
• $L$ = sequence length
• $D$ = 单向RNN时为1，双向RNN时为2
• $H_{in}$ = input_size
• $H_{out}$ = hidden_size

RNN的输出：

• output：当batch_first=False时输入形状为($L$,$N$,$D*H_{out}$)，当batch_first=True时输入形状为($L$,$N$,$D*H_{out}$)。
• h_n：形状为($D*num_layers$,$N$,$H_{out}$)。

RNN的权重和偏置矩阵:

• weight_ih_l[k]：第k层的输入权重矩阵。在K=0时形状为(hidden_size, input_size)，否则形状为(hidden_size,num_directions*hidden_size)。
• weight_hh_l[k]：第k层的隐藏状态权重矩阵。形状为(hidden_size, hidden_size)。
• bias_ih_l[k]：第k层的输入偏置值矩阵。形状为(hidden_size)。
• bias_hh_l[k]：第k层的隐藏状态偏置值矩阵。形状为(hidden_size)。

代码实现如下：

import torch
import torch.nn as nn

# 1.单向单层RNN
single_rnn = nn.RNN(4, 3, 1, batch_first=True)  # input_size, hidden_size, num_layers
input = torch.randn(1, 2, 4)  # batch_size * sequence length * feature_size
output, h_n = single_rnn(input)
print(output)
print(output.shape)  # [1, 2, 3] batch_size * sequence length * D*H_out
print(h_n)
print(h_n.shape)  # [1, 1, 3] D*num_layers * batch_size * H_out

# 2.双向单层RNN
bi_rnn = nn.RNN(4, 3, 1, batch_first=True, bidirectional=True)
input = torch.randn(1, 2, 4)
bi_output, bi_h_n = bi_rnn(input)
print(bi_output)
print(bi_output.shape)  # [1, 2, 6] batch_size * sequence length * D*H_out
print(bi_h_n)
print(bi_h_n.shape)  # [2, 1, 3] D*num_layers * batch_size * H_out

1.1.3 手写单向RNN

class MyRNN(nn.Module):
    def __init__(self, bs, T, input_size, hidden_size):
        super(MyRNN, self).__init__()

        self.bs = bs  # 批大小
        self.T = T  # 句子长度sequence length
        self.input_size = input_size  # 输入特征数
        self.hidden_size = hidden_size  # 隐藏状态特征数

        # 初始化权重和偏置值矩阵
        self.weight_ih = torch.ones(hidden_size, input_size, requires_grad=True)
        self.weight_hh = torch.ones(hidden_size, hidden_size, requires_grad=True)
        self.bias_ih = torch.zeros(hidden_size, requires_grad=True)
        self.bias_hh = torch.zeros(hidden_size, requires_grad=True)

    def forward(self, x, h_prev):
        h_out = torch.zeros(self.bs, self.T, self.hidden_size)

        for t in range(T):
            x = input[:, t, :]  # batch_size * input_szie
            # 切片之后x会变为2维，所以我们需要对x升维
            x = x.unsqueeze(2)  # batch_size * input_size * 1
            weight_ih_batch = self.weight_ih.unsqueeze(0).tile(bs, 1, 1)  # batch_size * hidden_size * input_size
            weight_hh_batch = self.weight_hh.unsqueeze(0).tile(bs, 1, 1)  # batch_size * hidden_size * hidden_size

            w_ih_times_x = torch.bmm(weight_ih_batch, x).squeeze(-1)  # batch_size * hidden_size
            w_hh_times_h = torch.bmm(weight_hh_batch, h_prev.unsqueeze(2)).squeeze(-1)  # batch_size * hidden_size
            h_prev = torch.tanh(w_ih_times_x + self.bias_ih + w_hh_times_h + self.bias_hh)

            h_out[:, t, :] = h_prev

        return h_out, h_prev.unsqueeze(0)


if __name__ == '__main__':
    bs, T = 2, 3  # 批大小，输入序列长度
    input_size, hidden_size = 2, 3  # 输入特征大小，隐藏状态特征大小
    input = torch.randn(bs, T, input_size)
    h_prev = torch.zeros(bs, hidden_size)  # [2, 3]
    
    myrnn = MyRNN(bs, T, input_size, hidden_size)
    my_rnn_output, my_state_final = myrnn(input, h_prev)

    print(my_rnn_output)
    print(my_state_final)

1.2 双向循环网络

1.2.1 双向RNN结构

单向循环网络只能依据之前时刻的时序信息来预测下一时刻的输出，但在有些问题中，当前时刻的输出不仅和之前的状态有关，还可能与未来的状态有关。
比如要预测一句话中缺失的单词时，就需要同时考虑上下文的内容。
双向RNN有两个RNN上下叠加在一起组成，输出由这两个RNN的状态共同决定。

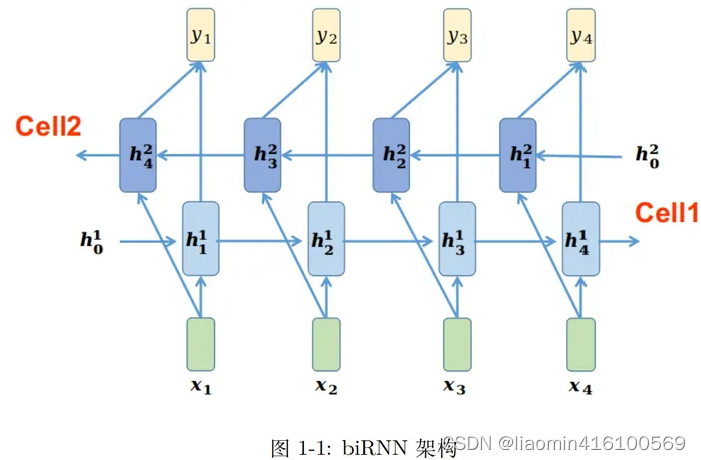
双向RNN的计算过程如下：

1. 首先进行前向RNN，输入$x_1$和$h_0^1$，输出$h_1^1$。
2. 再根据$x_2$和$h_2^1$计算得到$h_3^1$，以此类推进行完前向RNN。
3. 当前向RNN完成后计算反向RNN，反向RNN有单独的隐藏层$h_0^2$，且在反向RNN中输入input是反向输入的。
4. 首先输入$x_4$和$h_0^2$计算得到$h_1^2$，然后由$h_4^1$和$h_1^2$拼接得到最终输出的第一个输出$y_4$(可以直接拼接也可以相加得到$y_4$)。
5. 再由$x_3$和$h_1^2$得到$h_2^2$，由$h_3^1$和$h_2^2$拼接得到输出$y_3$。
6. 以此类推进行完反向RNN过程即可。

输入及输出分析：

• 输入：[$x_1,x_2,x_3,x_4$]
• forward输出：[$h_1^1,h_2^1,h_3^1,h_4^1$]
• backward输出：[$h_1^2,h_2^2,h_3^2,h_4^2$]
• 最终输出隐藏状态序列h_out：[$h_1^1|h_4^2,h_2^1|h_3^2,h_3^1|h_2^2,h_4^1|h_1^2$]
• 最终隐藏状态h_n：[$h_4^1,h_4^2$]

1.2.2 双向循环网络在pytorch中的实现

使用pytorch实现双向RNN只需要改变传入RNN的参数bidirectional=True即可。

import torch
import torch.nn as nn

bs, T = 2, 3  # 批大小，输入序列长度
input_size, hidden_size = 2, 3  # 输入特征大小，隐藏状态特征大小

input = torch.randn(bs, T, input_size)
h_prev = torch.zeros(2, bs, hidden_size)

bi_rnn = nn.RNN(input_size, hidden_size, batch_first=True, bidirectional=True)
bi_rnn_output, bi_state_final = bi_rnn(input, h_prev)

print(bi_rnn_output)
print(bi_state_final)

1.2.3 手写双向RNN

import torch
import torch.nn as nn


class MyBiRNN(nn.Module):
    def __init__(self, bs, T, input_size, hidden_size):
        super(MyBiRNN, self).__init__()
        self.bs = bs
        self.T = T
        self.input_size = input_size
        self.hidden_size = hidden_size

        # 初始化前向传播权重及偏置值矩阵
        self.weight_ih = torch.ones(self.hidden_size, self.input_size, requires_grad=True)
        self.weight_hh = torch.ones(self.hidden_size, self.hidden_size, requires_grad=True)

        self.bias_ih = torch.zeros(self.hidden_size, requires_grad=True)
        self.bias_hh = torch.zeros(self.hidden_size, requires_grad=True)
        # 初始化反向传播权重及偏置值矩阵
        self.weight_ih_reverse = torch.ones(self.hidden_size, self.input_size, requires_grad=True)
        self.weight_hh_reverse = torch.ones(self.hidden_size, self.hidden_size, requires_grad=True)

        self.bias_ih_reverse = torch.zeros(self.hidden_size, requires_grad=True)
        self.bias_hh_reverse = torch.zeros(self.hidden_size, requires_grad=True)

    def rnn_forward(self, input, weight_ih, h_prev, weight_hh, bias_ih, bias_hh):
        h_out = torch.zeros(self.bs, self.T, self.hidden_size)

        for t in range(self.T):
            x = input[:, t, :]  # batch_size * input_szie
            # 切片之后x会变为2维，所以我们需要对x升维
            x = x.unsqueeze(2)  # batch_size * input_size * 1
            weight_ih_batch = weight_ih.unsqueeze(0).tile(bs, 1, 1)  # batch_size * hidden_size * input_size
            weight_hh_batch = weight_hh.unsqueeze(0).tile(bs, 1, 1)  # batch_size * hidden_size * hidden_size

            w_ih_times_x = torch.bmm(weight_ih_batch, x).squeeze(-1)  # batch_size * hidden_size
            w_hh_times_h = torch.bmm(weight_hh_batch, h_prev.unsqueeze(2)).squeeze(-1)  # batch_size * hidden_size
            h_prev = torch.tanh(w_ih_times_x + bias_ih + w_hh_times_h + bias_hh)

            h_out[:, t, :] = h_prev

        return h_out, h_prev.unsqueeze(0)

    def forward(self, input, h_prev):
        h_out = torch.zeros(self.bs, self.T, self.hidden_size * 2)  # 双向RNN,所以特征是2倍

        # forward layer
        forward_output = self.rnn_forward(input, self.weight_ih, h_prev[0], self.weight_hh, self.bias_ih, self.bias_hh)[0]
        # backward layer
        # 反向传播时需要将输入反转，因为：
        # 假如输入为[x1,x2,x3,x4]，那么在backward中则是依次输入[x4,x3,x2,x1]
        backward_output = self.rnn_forward(torch.flip(input, [1]), self.weight_ih_reverse,
                                      h_prev[1], self.weight_hh_reverse, self.bias_ih_reverse,
                                      self.bias_hh_reverse)[0]

        # 拼接forward和backward的输出作为最后输出
        # h_out的前半部分是forward输出
        # h_out的后半部分是backward输出，因为backward是反向输出，所以需要翻转一下再拼接
        # 比如forward输出[h1^1,h2^1,h3^1,h4^1]，backward输出[h1^2,h2^2,h3^2,h4^2]
        # 最后拼接得到的是[h1^1|h4^2,h2^1|h3^2,h3^1|h2^2,h4^1|h1^2]
        h_out[:, :, :self.hidden_size] = forward_output
        h_out[:, :, self.hidden_size:] = torch.flip(backward_output, [1])

        # 最终状态应该是forward和backward各自的最终输出拼接在一起，即[h4^1|h4^2]
        h_n = torch.zeros(2, bs, hidden_size)
        h_n[0, :, :] = forward_output[:, -1, :]
        h_n[1, :, :] = backward_output[:, -1, :]

        return h_out, h_n


if __name__ == "__main__":
    bs, T = 2, 3  # 批大小，输入序列长度
    input_size, hidden_size = 2, 3  # 输入特征大小，隐藏状态特征大小

    input = torch.randn(bs, T, input_size)
    h_prev = torch.zeros(2, bs, hidden_size)

    my_bi_rnn = MyBiRNN(bs, T, input_size, hidden_size)
    my_bi_rnn_output, my_bi_state_final = my_bi_rnn(input, h_prev)
    print("my_bi_rnn_output:")
    print(my_bi_rnn_output)
    print("my_bi_state_final:")
    print(my_bi_state_final)

二、长短期记忆网络（LSTM）

传统的循环神经网络RNN虽然能够联系上下文的信息，但是RNN的梯度需要通过时间反向传播(Backpropagation Through Time)传播很长的时间步。当序列长度较大时，就会出现梯度消失或梯度爆炸的问题。这种问题可能会导致某些不太重要的信息对其后续信息的预测造成影响。
所以我们引入了“长短期记忆”(long-short-term memory, LSTM)和“门控循环单元”(gated recurrent unit,GRU)。
传统的RNN对于输入的重要性判断很固定，越早输入的越不重要，越晚输入的越重要，这显然存在一定的问题。而LSTM则是通过门控制的方式实现了对输入重要度的控制。

2.1 LSTM结构

原始的RNN隐藏状态只有一个$h$，它对于短期输入非常敏感，所以我们的想法就是增加一个隐藏状态$c$用来保存长期状态，我们把状态$c$称为候选记忆单元，这就是LSTM。
LSTM的结构如下图：

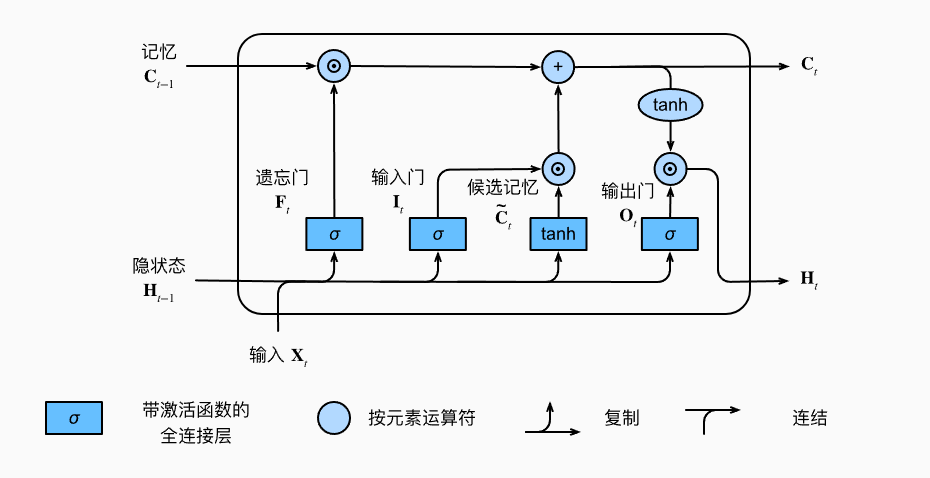
LSTM的公式如下：

$$i_t = \sigma(W_{ii}x_t + b_{ii} + W_{hi}h_{t-1} + b_{hi}) \hspace{0.8cm}\\ f_t = \sigma(W_{if}x_t + b_{if} + W_{hf}h_{t-1} + b_{hf}) \hspace{0.55cm}\\ g_t = tanh(W_{ig}x_t + b_{ig} + W_{hg}h_{t-1} + b_{hig}) \\ o_t = \sigma(W_{io}x_t + b_{io} + W_{ho}h_{t-1} + b_{ho}) \hspace{0.6cm}\\ c_t = f_t \odot c_{t-1} + i_t \odot g_t \hspace{2.65cm}\\ h_t = o_t \odot tanh(c_t) \hspace{3.25cm}$$

LSTM中有三种门：$i_t$是输入门，它控制使用多少来自候选记忆单元$g_t$的数据，遗忘门$f_t$控制保留多少过去的记忆元$c_{t-1}$的内容，输出门$o_t$用于决定当前时刻输出哪些信息。
公式中的激活函数$\sigma$(即sigmoid)和$tanh$目的都是将输出限制在[0,1]之间。

2.2 手写LSTM

LSTM的实现与RNN类似，但是需要注意的是，因为我们在$i_t,f_t,g_t,o_t$中都要实现$W_ix_t$和$W_hx_t$，所以我们可以将四个权重矩阵拼接到一起，然后只进行一次矩阵乘法运算即可。

import torch
import torch.nn as nn


# 手写LSTM
class MyLSTM(nn.Module):
    def __init__(self, bs, T, input_size, hidden_size):
        super(MyLSTM, self).__init__()

        self.bs = bs
        self.T = T
        self.input_size = input_size
        self.hidden_size = hidden_size

        # 由于是四个权重矩阵拼接在一起，所以一共是4*hidden_szie行
        self.weight_ih = nn.Parameter(
            torch.Tensor(4 * self.hidden_size, self.input_size))  # (4*hidden_size, input_size)
        self.weight_hh = nn.Parameter(
            torch.Tensor(4 * self.hidden_size, self.hidden_size))  # (4*hiddden_size, hidden_size)
        # 偏置矩阵同理
        self.bias_ih = nn.Parameter(torch.Tensor(4 * hidden_size))
        self.bias_hh = nn.Parameter(torch.Tensor(4 * hidden_size))

        # 初始化权重
        nn.init.xavier_uniform_(self.weight_ih)
        nn.init.orthogonal_(self.weight_hh)
        nn.init.zeros_(self.bias_ih)
        nn.init.zeros_(self.bias_hh)

    def forward(self, input, initial_states):
        h_0, c_0 = initial_states
        bs, T, input_size = input.shape
        hidden_size = self.weight_ih.shape[0] // 4

        prev_h = h_0
        prev_c = c_0
        # 权重矩阵扩维
        # w_ih.shape = (4*hidden_size ,input_size)
        # w_hh.shape = (4*hidden_szie, hidden_size)
        bath_w_ih = self.weight_ih.unsqueeze(0).tile(bs, 1, 1)  # (bs, 4*hidden_size, inputsize)
        bath_w_hh = self.weight_hh.unsqueeze(0).tile(bs, 1, 1)  # (bs, 4*hiddden_size, hidden_size)

        output = torch.zeros(bs, T, hidden_size)

        for t in range(T):
            x = input[:, t, :]
            x = x.unsqueeze(-1)  # 升维

            w_times_x = torch.bmm(bath_w_ih, x).squeeze(-1)  # (bs, 4*hidden_szie)
            w_times_prev_h = torch.bmm(bath_w_hh, prev_h.unsqueeze(-1)).squeeze(-1)  # (bs, 4*hidden_size)

            # 输入门
            i_t = torch.sigmoid(w_times_x[:, :hidden_size] + self.bias_ih[:hidden_size] +
                                w_times_prev_h[:, :hidden_size] + self.bias_hh[:hidden_size])
            # 遗忘门
            f_t = torch.sigmoid(w_times_x[:, hidden_size:2 * hidden_size] + self.bias_ih[hidden_size:2 * hidden_size] +
                                w_times_prev_h[:, hidden_size:2 * hidden_size] + self.bias_hh[
                                                                                 hidden_size:2 * hidden_size])

            g_t = torch.tanh(
                w_times_x[:, 2 * hidden_size:3 * hidden_size] + self.bias_ih[2 * hidden_size:3 * hidden_size] +
                w_times_prev_h[:, 2 * hidden_size:3 * hidden_size] + self.bias_hh[2 * hidden_size:3 * hidden_size])
            # 输出门
            o_t = torch.sigmoid(w_times_x[:, 3 * hidden_size:] + self.bias_ih[3 * hidden_size:] +
                                w_times_prev_h[:, 3 * hidden_size:] + self.bias_hh[3 * hidden_size:])

            prev_c = f_t * prev_c + i_t * g_t
            prev_h = o_t * torch.tanh(prev_c)
            output[:, t, :] = prev_h

        return output, [prev_h, prev_c]


if __name__ == "__main__":
    bs, T, input_size, hidden_size = 2, 3, 4, 5
    input = torch.randn(bs, T, input_size)
    c_0 = torch.randn(bs, hidden_size)
    h_0 = torch.randn(bs, hidden_size)

    mylstm = MyLSTM(bs, T, input_size, hidden_size)
    my_output, (my_h_final, my_c_final) = mylstm(input, (h_0, c_0))

    print("My LSTM")
    print(my_output)
    print(my_h_final, my_c_final)

三、门控循环单元（GRU）

GRU的实现原理与LSTM类似，只不过GRU对LSTM做了一些优化，减少了一些参数。

3.1 GRU结构

GRU通过引入重置门(reset gate)和更新门(update gate)来实现对重要度不同信息的控制。重置门控制前一时刻隐藏状态对当前时刻候选隐藏状态的影响程度，更新们控制上一时刻的隐藏状态($h_{t-1}$)与当前候选隐藏状态($\tilde{h_{t}}$)的混合程度，决定信息的保留和更新比例。
GRU的结构如下图：

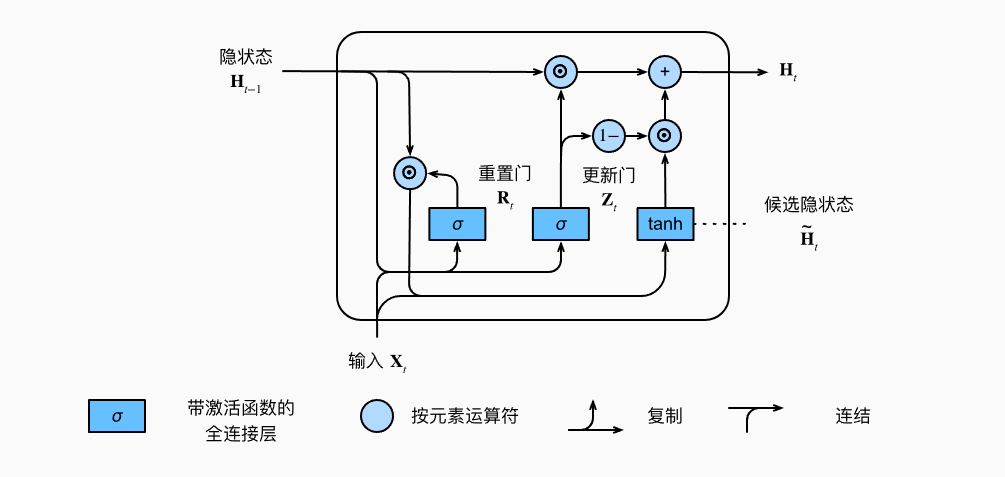
GRU的公式如下：

$$r_t = \sigma(W_{ir}x_t + b_{ir} + W_{hr}h_{t-1} + b_{hr}) \hspace{1.65cm}\\ z_t = \sigma(W_{iz}x_t + b_{iz} + W_{hz}h_{t-1} + b_{hz}) \hspace{1.65cm}\\ n_t = tanh(W_{in}x_t + b_{in} + r_t \odot (W_{hn}h_{t-1} + b_{hn})) \\ h_t = (1-z_t) \odot n_t + z_t \odot h_{t-1} \hspace{2.65cm}$$

我们通过$r_t$来计算候选隐藏状态$n_t$，然后再根据$z_t$控制候选隐藏状态与前一隐藏状态的比例，从而计算得到新的隐藏状态$h_t$。

3.2 手写GRU

GRU的实现与LSTM非常类似，只不过参数变为了LSTM的$\frac{3}{4}$:

import torch
import torch.nn as nn


# 手写GRU
class MyGRU(nn.Module):
    def __init__(self, bs, T, input_size, hidden_size):
        super(MyGRU, self).__init__()

        self.bs = bs
        self.T = T
        self.input_size = input_size
        self.hidden_size = hidden_size

        # 由于是三个权重矩阵拼接在一起，所以一共是3*hidden_szie行
        self.weight_ih = nn.Parameter(torch.Tensor(3 * self.hidden_size, self.input_size))  # (3*hidden_size, input_size)
        self.weight_hh = nn.Parameter(torch.Tensor(3 * self.hidden_size, self.hidden_size))  # (3*hiddden_size, hidden_size)
        # 偏置矩阵同理
        self.bias_ih = nn.Parameter(torch.Tensor(3 * hidden_size))
        self.bias_hh = nn.Parameter(torch.Tensor(3 * hidden_size))

        # 初始化权重
        nn.init.xavier_uniform_(self.weight_ih)
        nn.init.orthogonal_(self.weight_hh)
        nn.init.zeros_(self.bias_ih)
        nn.init.zeros_(self.bias_hh)

    def forward(self, input, h_prev):
        # 初始化输出矩阵
        output = torch.zeros(self.bs, self.T, self.hidden_size)

        # 权重矩阵升维
        bath_w_ih = self.weight_ih.unsqueeze(0).tile(self.bs, 1, 1)  # (bs, 3*hiddden_size, input_size)
        bath_w_hh = self.weight_hh.unsqueeze(0).tile(self.bs, 1, 1)  # (bs, 3*hiddden_size, hidden_size)

        # 递归计算每个时间步
        for t in range(self.T):
            x = input[:, t, :]  # (bs, input_size)
            # x切片后是2维，由于权重为3维，所以x也需要升维
            x = x.unsqueeze(-1)  # (bs, input_size, 1)

            # 计算W*x和W*h_prev
            w_times_x = torch.bmm(bath_w_ih, x)  # (bs, 3*hidden_size, 1)
            w_times_x = w_times_x.squeeze(-1)  # (bs, 3*hidden_size)
            w_times_h_prev = torch.bmm(bath_w_hh, h_prev.unsqueeze(-1))  # (bs, 3*hidden_size, 1)
            w_times_h_prev = w_times_h_prev.squeeze(-1)  # (bs, 3*hidden_size)

            # 计算重置门和更新门
            r_t = torch.sigmoid(w_times_x[:, :self.hidden_size] + self.bias_ih[:self.hidden_size] +
                                w_times_h_prev[:, :self.hidden_size] + self.bias_hh[:self.hidden_size])
            z_t = torch.sigmoid(w_times_x[:, self.hidden_size:2 * self.hidden_size] + self.bias_ih[self.hidden_size:2 * self.hidden_size] +
                                w_times_h_prev[:, self.hidden_size:2 * self.hidden_size] + self.bias_hh[self.hidden_size:2 * self.hidden_size])

            # 计算候选隐藏状态
            n_t = torch.tanh(w_times_x[:, 2 * self.hidden_size:] + self.bias_ih[2 * self.hidden_size:] +
                             r_t * (w_times_h_prev[:, 2 * self.hidden_size:] + self.bias_hh[2 * self.hidden_size:]))

            # 更新最隐藏状态
            h_prev = (1 - z_t) * n_t + z_t * h_prev
            output[:, t, :] = h_prev

        return output, h_prev


if __name__ == "__main__":
    bs, T, input_size, hidden_size = 2, 3, 4, 5
    input = torch.randn(bs, T, input_size)
    h_prev = torch.randn(bs, hidden_size)

    # 调用API
    gru = nn.GRU(input_size, hidden_size, batch_first=True)
    output, h_final = gru(input, h_prev.unsqueeze(0))

    mygru = MyGRU(bs, T, input_size, hidden_size)
    my_output, my_h_final = mygru(input, h_prev)

    print(output.shape == my_output.shape)
    # print(my_output)
    # print(my_h_final)

参考资料：
[1] Pytorch官方文档
[2] PyTorch RNN的原理及其手写复现
[3] 如何从RNN起步，一步一步通俗理解LSTM
[4] 循环神经网络 RNN【动手学深度学习v2】
[5] 深度学习05-RNN循环神经网络