Directional diffusion models for graph representation learning

论文地址：Directional diffusion models for graph representation learning

Introduction

本文主要研究的是如何让diffusion model更好的应用于图学习领域。
Diffusion model已经可以很好地处理图像（image）数据，那么为什么diffusion model不能直接用于处理图（graph）数据呢？这里首先要说明一下image和graph的区别。
在本文中作者对图像数据和图数据采用了奇异值分解(SVD)的方法，并在二维平面上可视化投影数据，如下图所示：
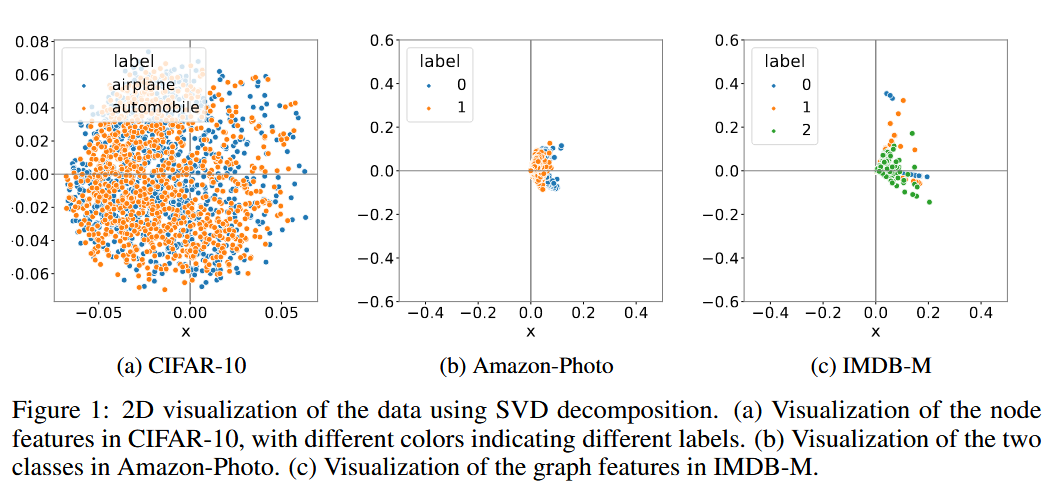
figure 1
从实验结果我们可以看出，图像数据（CIFAR-10）在以原点为中心的圆形形状内形成了相对更各向同性的分布，而图数据（Amazon-Photo和IMDB-M）仅在几个方向上表现出强烈的各向异性结构。
在经典的diffusion model中，我们项数据中添加的噪声一般都是高斯噪声，而高斯噪声与图像数据一样具有各向同性，所以随着噪声的不断添加，图像会逐渐转变为具有各向同性的白噪声。这种方法是合理的。因为它逐渐将数据转化为噪声，生成具有宽信噪比的噪声样本序列。
但是由于图数据是各向异性的，所以当我们添加各向同性的高斯噪声时，原来的数据会被迅速地污染，这使得信噪比迅速下降并接近0。因此，经典的diffusion model很难用于处理图数据。
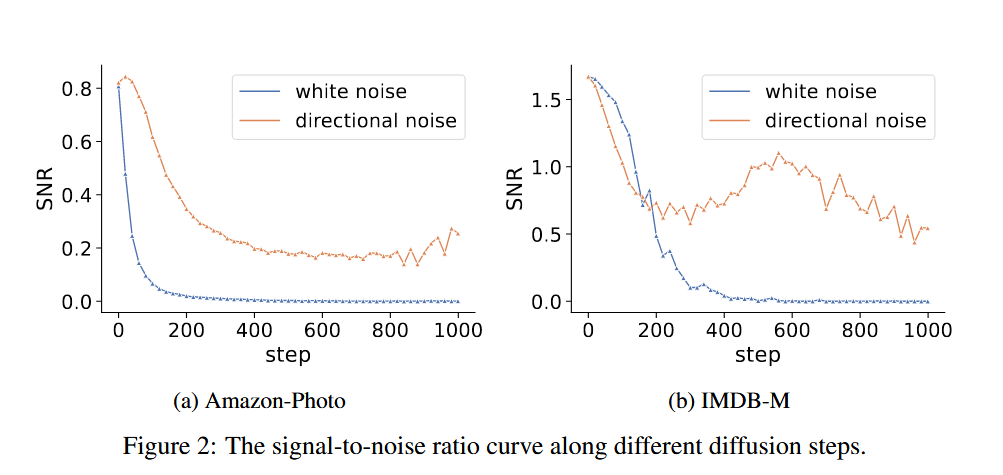
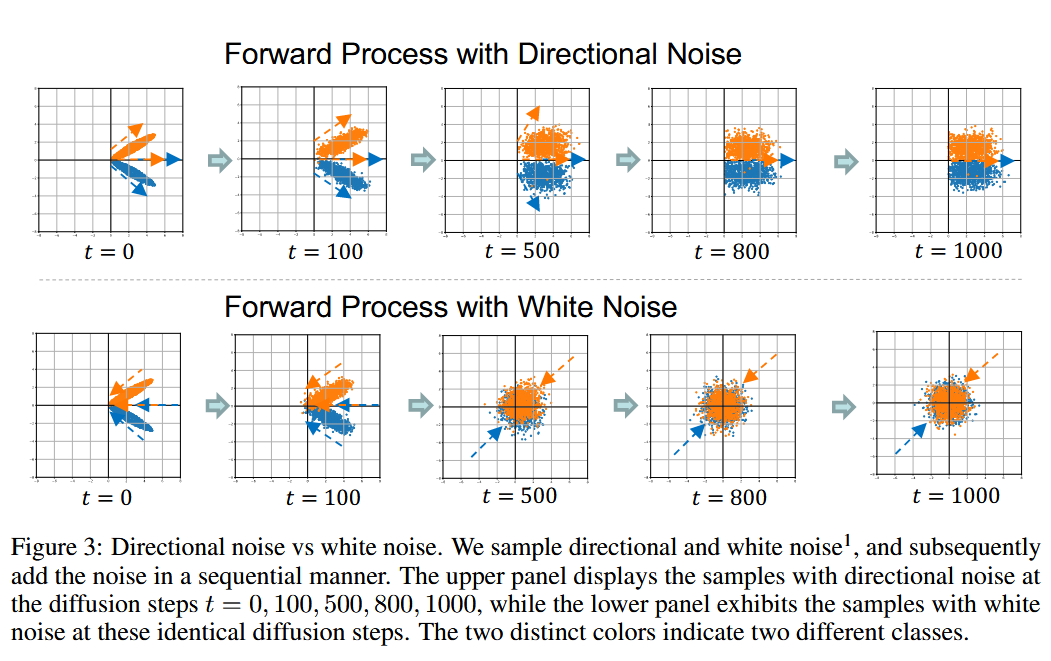
既然添加各向同性噪声不好，那么我们可不可以根据图数据表现出的各向异性来添加具有同样各向异性的噪声呢，答案是肯定的这也就是本篇论文的核心：directional noise(定向噪声)。当我们添加定向噪声时，信噪比就会下降的比较慢，这种较慢的下降就使得能够提取具有不同信噪比的细粒度特征表示，从而保留各向异性的基本信息。作者所做的关于信噪比随噪声变化的实验也说明了这点。
figure 2
figure 3

Directional diffusion models

本文提出的定向扩散模型（DDM）具体长这样：
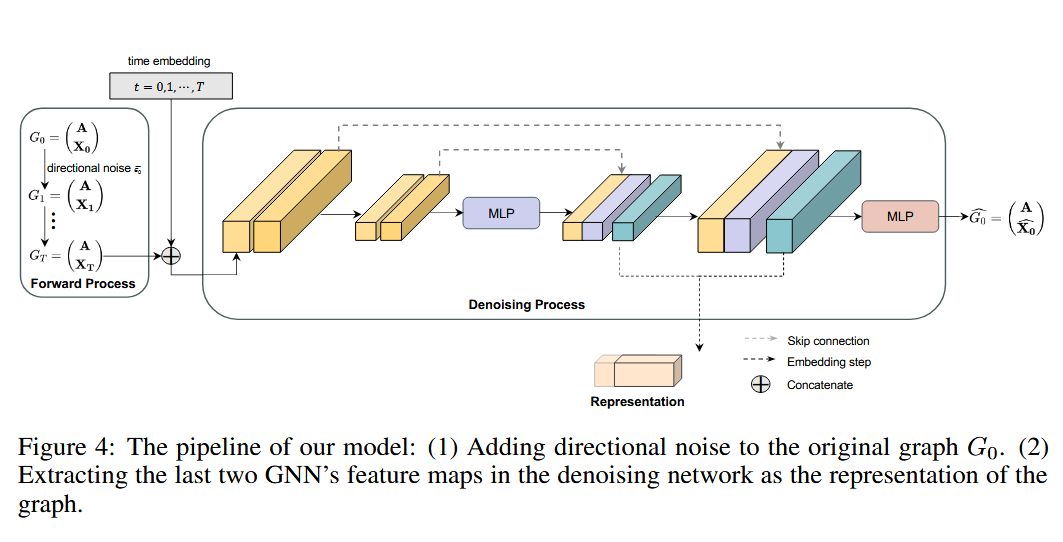
figure 4
它一共使用了4个GNN层和一个多层感知机(MLP)。其中，前两个GNN层作为编码器，负责通过聚合邻接信息来去噪目标节点。最后两个GNN层作为解码器，将去噪后的节点特征映射到隐含码并平滑相邻节点之间的隐含码。为了解决过度平滑的问题并考虑图中的长距离依赖关系，作者还在编码器和解码器之间引入了跳接。

符号表示

我们使用G=(V,A,X)G=(V,A,X)表示一个图，其中：VV表示节点集，N=∣V∣N=|V|表示结点个数，A∈RN×NA \in \Reals^{N×N}表示图的邻接矩阵，X=(x1,x2,...,xN)T∈RN×dX=(x_1,x_2,...,x_N)_T \in \Reals^{N×d}表示节点的特征矩阵。
我们的目标是学习一个网络f:RN×d×RN×N→RN×dhf:\Reals^{N×d} × \Reals^{N×N} \to \Reals^{N × d_h}，它可以将图的特征编码为表示H=(h1,h2，...，hN)T∈RN×dhH = (h_1, h_2，...，h_N)^T \in \Reals^{N × d_h}，其中hi∈Rdhh_i \in \Reals^{d_h}是节点ii的表示。从数学上讲，我们有H=f(X,A)H = f(X, A)，这些表示可以用于下游任务，如图和节点分类。

Directional diffusion models

Training

DDM在前向扩散过程中与DDPM类似，都是可以使用原图x0x_0以及噪声ϵ\epsilon直接得到时间tt时的图片，但与DDPM中不同的是，在DDM中我们添加的是定向噪声，所以具体的添加过程如下面公式所示：

xt,i=αˉtx0,i+1−αˉtϵ′ϵ′=sgn(x0,i)⊙∣ϵˉ∣ϵˉ=μ+σ⊙ϵ  where ϵ∼N(0,I)\begin{align*} x_{t,i} &= \sqrt{\bar\alpha_t}x_{0,i} + \sqrt{1-\bar\alpha_t}\epsilon' \tag{1} \newline \epsilon' &= sgn(x_{0,i}) \odot |\bar\epsilon| \tag{2} \newline \bar\epsilon &= \mu + \sigma \odot\epsilon &\ &\ where &\ \epsilon \sim \mathcal{N}(0,\Iota) \tag{3} \end{align*}

其中公式(1)与DDPM中一样，而公式(3)是为了将与数据无关的高斯噪声ϵ\epsilon转换为各向异性和批相关的噪声ϵˉ\bar\epsilon，其中μ\mu和σ\sigma是NN个节点上dd个特征的均值和标准差。公式(2)是为了将噪声的方向与特征x0,ix_{0,i}对齐。通过这三个公式我们就实现了在数据中添加定向噪声的目的。
公式(2)(3)约束协同工作，以确保正向扩散过程尊重底层数据结构，并减轻信号的快速退化。因此，信噪比衰减缓慢，使我们的定向扩散模型能够在各个步骤中有效地提取有意义的特征表示。这反过来又通过提供可靠性和信息性来增强这些表示在下游任务中的实用性。
至于损失函数，DDP采用了与DDPM相同的损失函数，也就是先根据输入的数据Xt,A,tX_t,A,t使用fθf_\theta预测得到预测结果，再计算预测结果与X0X_0的欧几里得距离:

L=𝔼X0,t∣∣fθ(Xt,A,t)−X0∣∣2(4)\mathcal{L} = \char"1D53c_{X_{0,t}}||f_\theta(X_t,A,t)-X_0||^2 \tag{4}

训练过程的伪代码如下：
The training algorithm

Extracting representations

提取表征的过程如下：
Extracting representation
我们首先计算节点特征的均值μ\mu和标准差σ\sigma，然后对于每一个时间步kk，我们都根据公式(1)引入kk步的定向噪声得到XkX_k，并使用预训练得到的降噪网络fθf_\theta来对噪声数据XkX_k进行降噪和编码。fθf_\theta的解码器将去噪节点特征映射为一个潜码，同时平滑相邻节点之间的潜码。
最后我们从fθf_\theta的解码器中提取激活然后再将它们拼接起来就得到了最后的表征Hk=hk,1,hk,2,...,hk,N∈RN×dhH_k={h_{k,1},h_{k,2},...,h_{k,N}} \in \Reals^{N×d_h}。

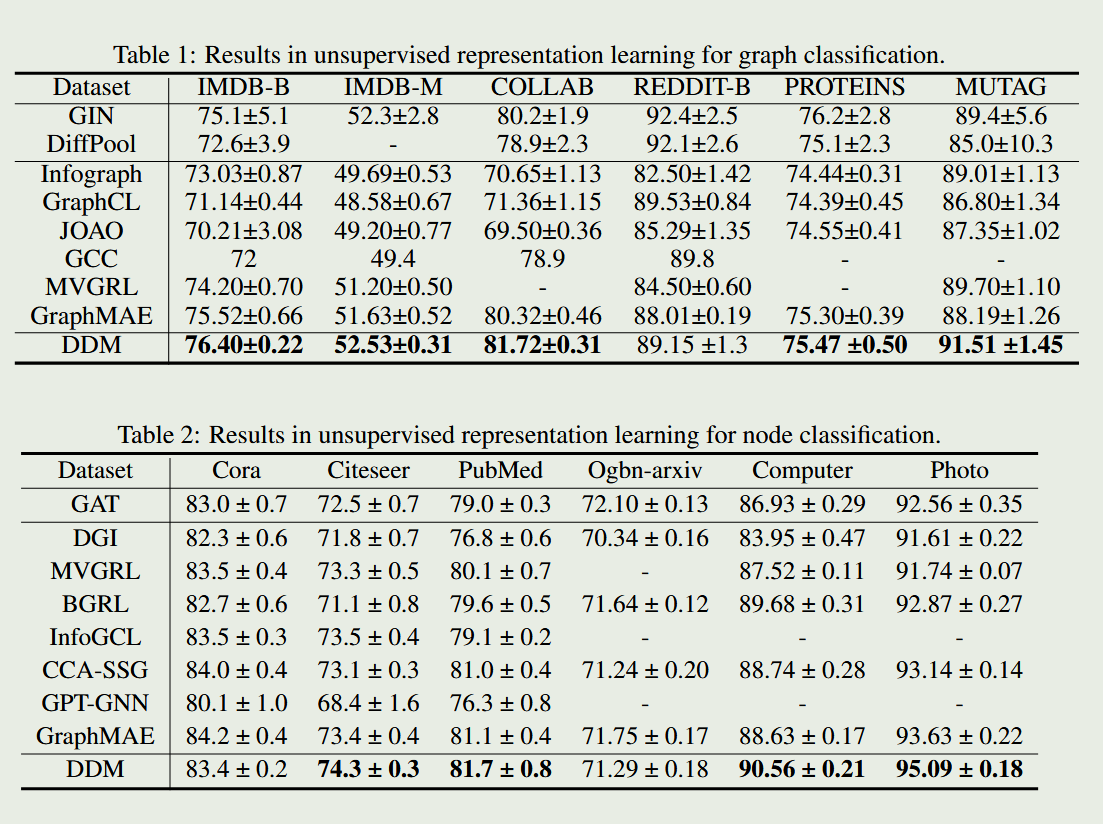
Experiments

实验表明，通过添加定向噪声，确实可以大幅提高diffusion model在处理图数据问题时的准确性。
Experiments