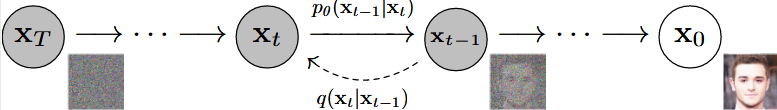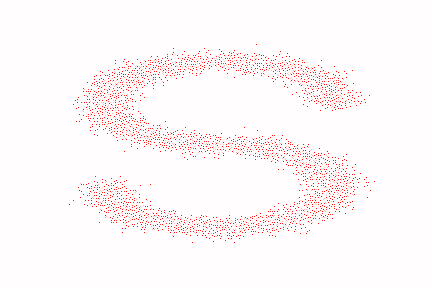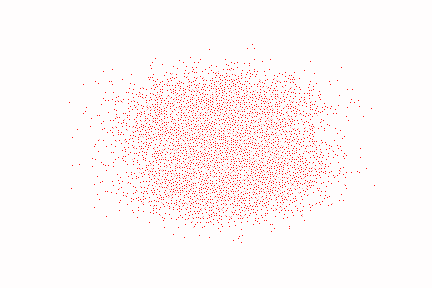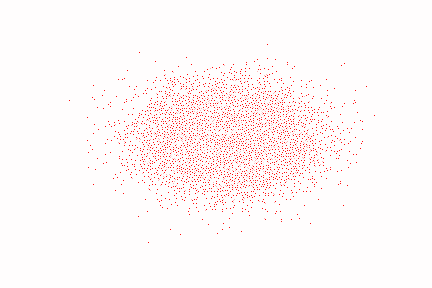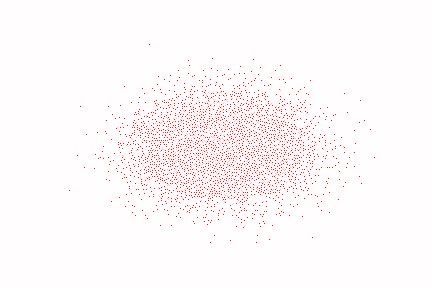Diffusion Model原理及代码解析

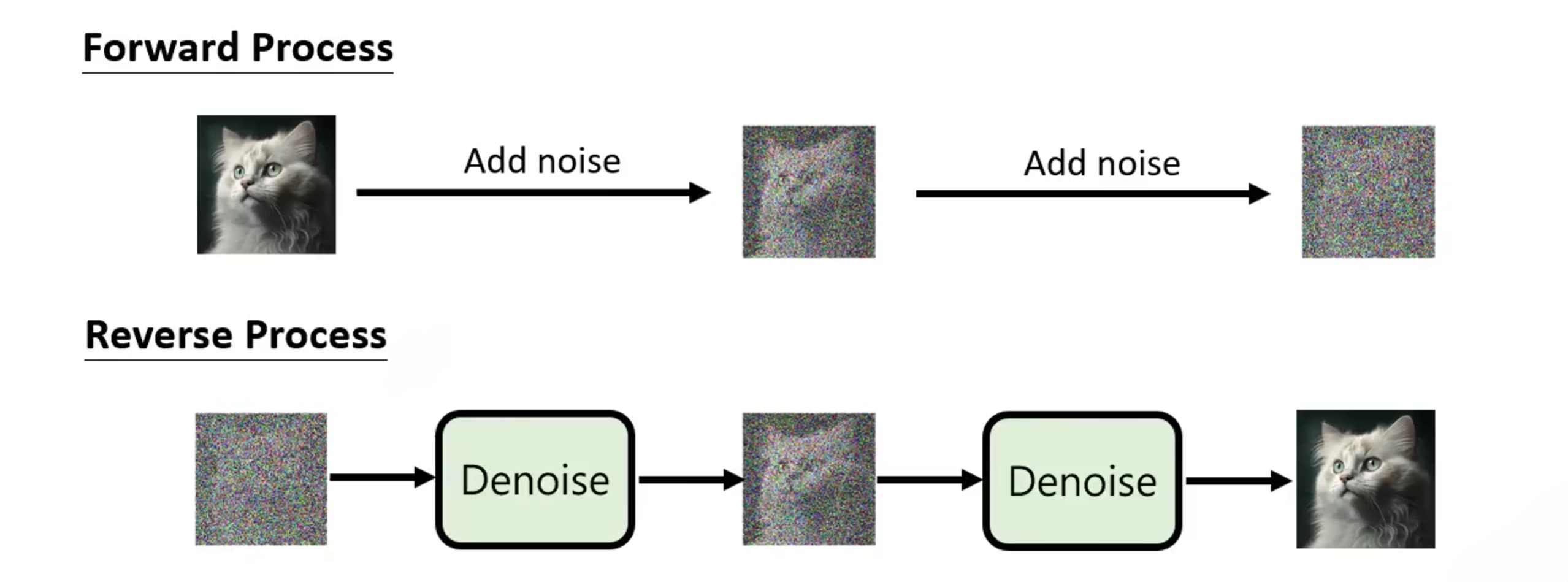
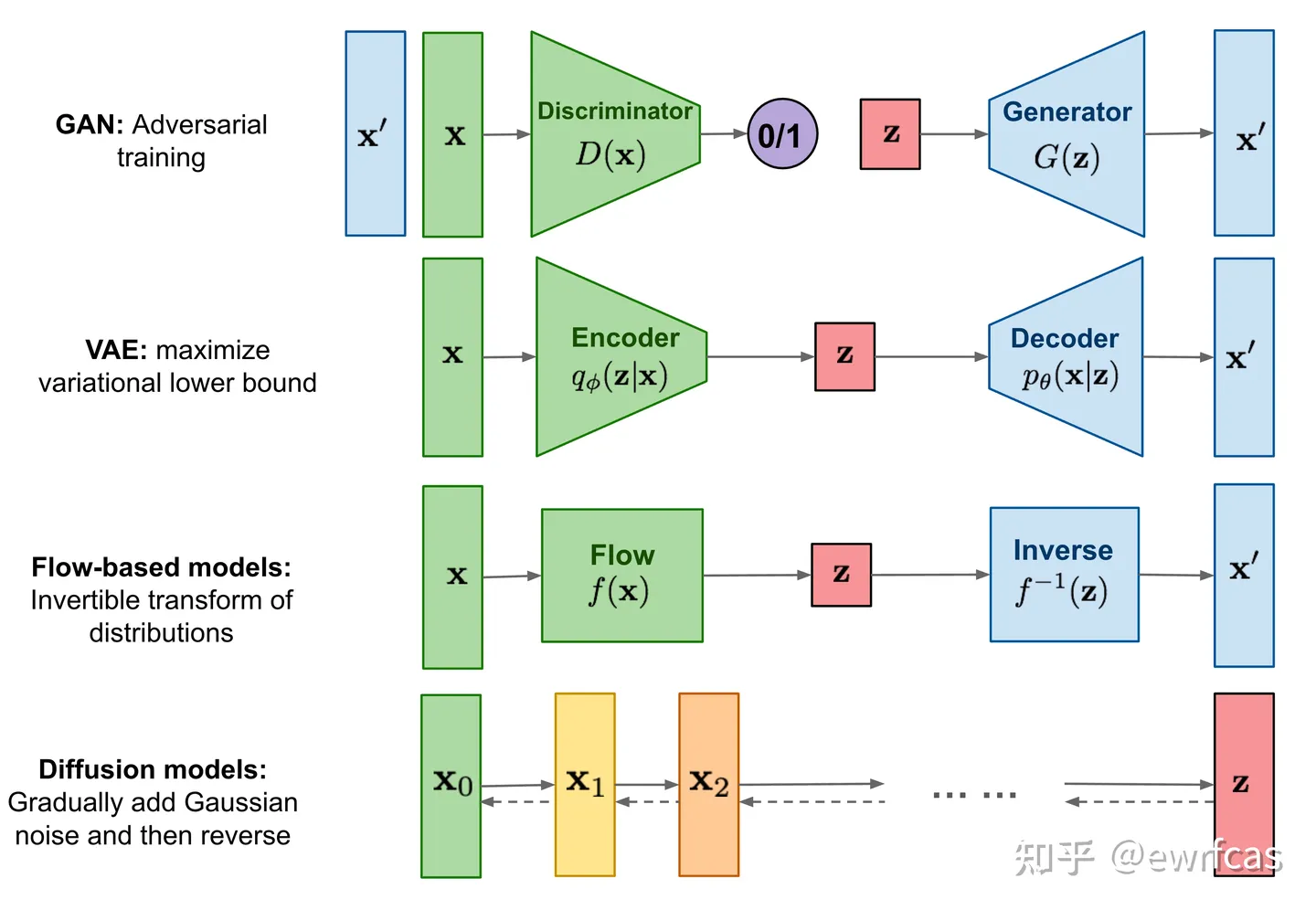
扩散模型（Diffusion Model）是一类生成模型，用于学习如何从噪声中生成数据。近年来，它们在图像生成、文本生成等领域取得了显著的进展。扩散模型的基本思想是通过逐步向数据添加噪声（通常是高斯噪声），让数据逐渐变得模糊，直至接近纯噪声的形式。然后，模型通过学习逆向过程，即从噪声逐步恢复出原始数据，从而生成新的样本。

目前有很多生成模型，比如GAN，VAE，Flow-based models，Diffusion models等等:

本文主要介绍的模型是Denoising Diffusion Probabilistic Models。

一、基础知识

1.1 条件概率的一般形式

$$\begin{align} P(A,B,C)=P(C|B,A)P(B,A)=P(C|B,A)P(B|A)P(A) \tag{1-1} \newline P(B,C|A)=P(B|A)P(C|A,B) \tag{1-2}\hspace{4.25cm} \end{align}$$

1.2 基于马尔科夫链假设的概率

马尔科夫链假设：简单来说就是研究对象在$t$时刻的状态只与$t-1$时刻的状态有关，而与之前的状态无关。
若满足马尔科夫链关系：$A \to B \to C$，则有：

$$\begin{align*} P(A,B,C)=P(C|B,A)P(B,A)=P(C|B)P(B|A)P(A) \tag{1-3}\newline P(B,C|A)=P(B|A)P(C|B) \hspace{4.25cm} \tag{1-4} \end{align*}$$

1.3 贝叶斯公式

$$P(A|B)=P(B|A)\frac{P(A)}{P(B)} \tag{1-5}$$

1.4 高斯分布的KL散度公式

相对熵（relative entropy），又被称为Kullback-Leibler散度（Kullback-Leibler divergence）或信息散度（information divergence），是两个概率分布（probability distribution）间差异的非对称性度量。在信息理论中，相对熵等价于两个概率分布的信息熵（Shannon entropy）的差值。
对于两个单一变量的高斯分布$p$和$q$而言，他们的KL散度为：

$$KL(p,q)=log\frac{\sigma_2}{\sigma_1}+\frac{\sigma_1^2+(\mu_1-\mu_2)^2}{2\sigma_2^2}-\frac{1}{2} \tag{1-6}$$

其中：

$$p \thicksim \mathcal{N}(\mu_1,\sigma_1^2) \newline q \thicksim \mathcal{N}(\mu_2,\sigma_2^2)$$

1.5 重参数化技巧（Reparameterization Trick）

重参数化技巧（Reparameterization Trick） 是一种在深度学习中常用的技术，尤其是在变分自动编码器（Variational Autoencoder, VAE）中，用来解决对随机变量进行梯度求导的问题。

1.5.1 重参数化的核心思想

重参数化的核心思想是将一个随机变量的采样过程表示为一个确定性函数加上一些外部噪声。通过这种方式，我们能够将梯度传播到随机变量的参数上。
具体来说，假设我们有一个高斯分布$z \sim \mathcal{N}(\mu, \sigma^2)$，传统的采样方法会直接从这个高斯分布中生成样本$z$，但这样做时，$z$的生成过程包含了随机性，不能直接对$\mu$和$\sigma$求梯度，因为采样操作不可导。
重参数化技巧的核心思想是： 将$z$的采样过程重新表示为一个确定性函数形式：

$$z = \mu + \sigma \cdot \epsilon \tag{1-7}$$

其中，$\epsilon$是从标准正态分布$\epsilon \sim \mathcal{N}(0,1)$中采样的。通过这种变换，随机性被分离到了$\epsilon$中，而$z$现在是由$\mu$和$\sigma$确定性地生成的。这样，虽然我们在计算$z$时仍然依赖噪声$\epsilon$，但这个公式对$\mu$和$\sigma$是可导的，可以通过反向传播计算出损失函数对$\mu$和$\sigma$的梯度。
需要注意的是：重参数化只是将采样过程重写为可导的形式，而没有改变分布本身，$z$依然服从于正态分布$\mathcal{N}(\mu, \sigma^2)$。

1.5.2 重参数化的优势

1. 可导性：
   通过将随机变量表示为确定性变量的函数，重参数化技巧使得我们能够对采样过程进行梯度求解，从而可以使用常规的反向传播算法来优化目标函数。
2. 稳定性：
   重参数化技巧将采样和参数分离，使模型在优化时更稳定。例如，在VAE中，通过这种技巧可以更有效地学习潜在空间的分布。
3. 高效性：
   通过重参数化，我们可以避免复杂的蒙特卡罗方法，减少计算量并加快模型的训练速度。

1.5.3 示例

假设我们要优化一个由高斯分布$\mathcal{N}(\mu, \sigma^2)$生成的随机变量$z$，我们希望通过最小化某个损失函数$L(z)$来学习$\mu$和$\sigma$。直接对$z$进行优化很难，但通过重参数化：

$$z = \mu + \sigma \cdot \epsilon, \epsilon \sim \mathcal{N}(0,1)$$

我们可以将损失函数$L(z)$写成$L(\mu + \sigma \cdot \epsilon)$，然后通过反向传播来计算关于$\mu$和$\sigma$的梯度。

二、Diffusion扩散过程

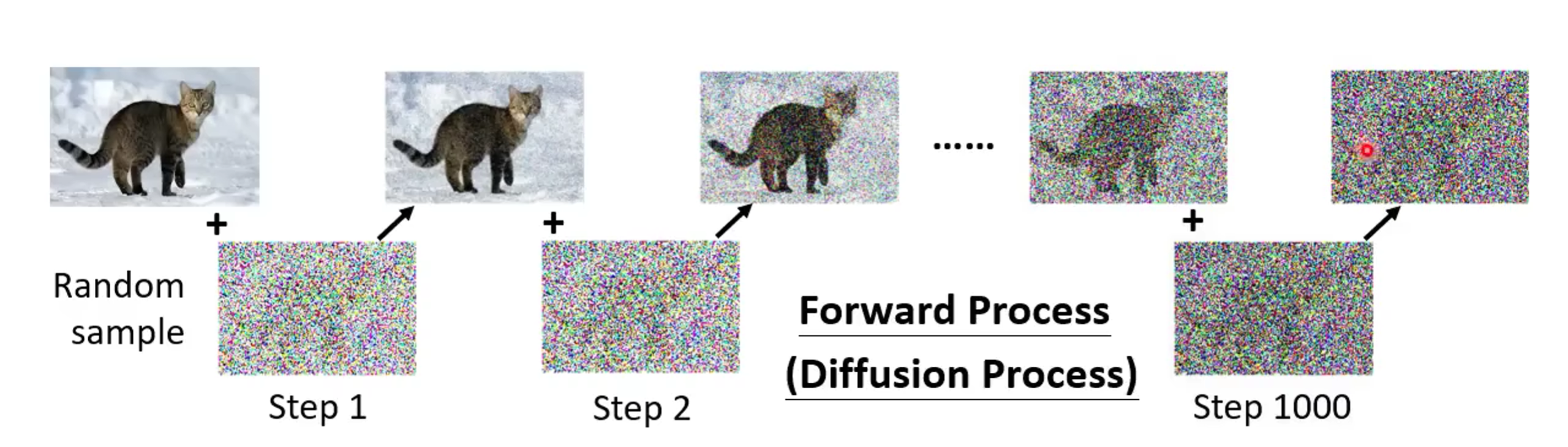
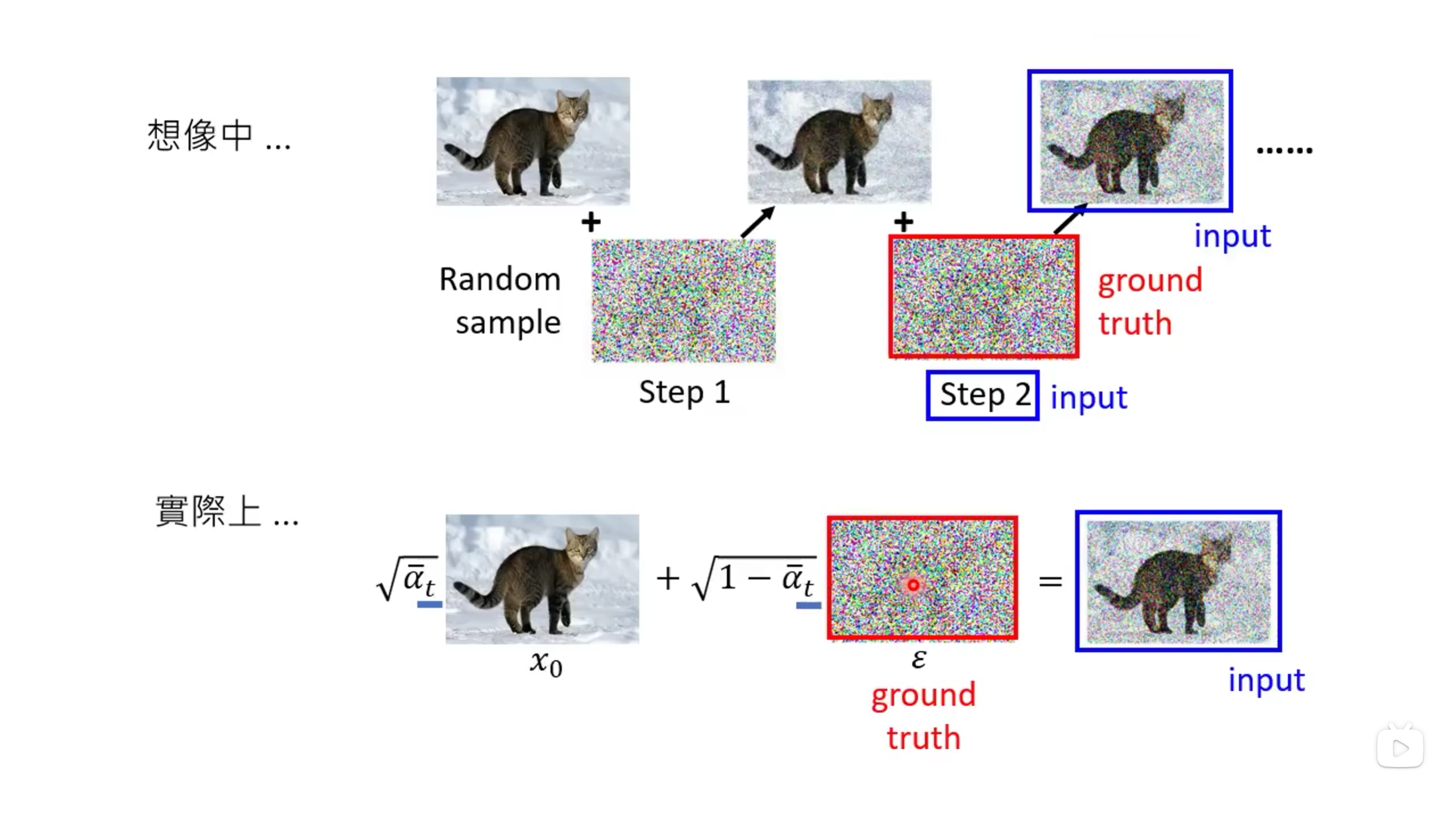
2.1 Diffusion正向扩散过程（Forward Process）

Diffsion model的正向传播过程是一个向图片添加噪音的过程。

给定初始数据分布$x_0 \sim q(x)$，可以不断向分布中添加$T$次高斯噪声，得到$x_1,x_2,...,x_T$，如下图的$q$过程。这里需要给定一系列的高斯分布方差的超参数$\{\beta_t \in (0,1)\}_{t=1}^T$。假设每次添加噪声的过程符合马尔科夫链假设，则有：

$$\begin{align*} q(x_t|x_{t-1})=\mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1},\beta_t\Iota)\tag{2-1} \newline q(x_{1:T}|x_0)=\prod_{t=1}^Tq(x_t|x_{t-1}) \tag{2-2}\hspace{1.55cm} \end{align*}$$

其中，$\beta_t$是随着$t$的增大而逐渐变大的，在原论文中，$\beta_t \in (0.0001,0.02)$。也就是说，在前向扩散过程中，随着$t$的增大，$\beta_t$不断增大，也就是噪声的占比逐渐变多，$x_t$越来越接近纯噪声。当$T \to \infin$时，$x_T$是完全的高斯噪声。

利用重参数技巧我们可以将添加噪声的过程用下面的公式表示：

$$x_t = \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_{t-1} \tag{2-3}$$

其中：$x_t$表示$t$时刻的图像，$x_{t-1}$表示$t-1$时刻的图像，$z_{t-1}$表示$t-1$时刻添加的高斯噪声，其服从于高斯分布$\mathcal{N}(0,1)$。$\alpha_t=1-\beta_t$。
当我们不断带入前一时刻的表达式后可以得到：

$$\begin{align*} x_t &= \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z_{t-1} \\ &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}z_{t-2})+\sqrt{1-\alpha_t}z_{t-1} \\ &= \sqrt{\alpha_t\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_t\alpha_{t-1}}z_{t-2} \\ &= ... \\ &= \sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\bar{z_t} \tag{2-4} \end{align*}$$

其中:$\bar \alpha_t=\prod_{i=1}^T\alpha_i$，$\bar{z_t} \sim \mathcal{N}(0,1)$。
注意：在第三行中我们使用了一个技巧：两个正态分布$X \sim \mathcal{N}(\mu_1,\sigma_1^2)$和$Y \sim \mathcal{N}(\mu_2,\sigma_2^2)$叠加后的分布$aX+bY$的均值为$a\mu_1+b\mu_2$，方差为$a^2\sigma_1^2+b^2\sigma_2^2$，所以$\sqrt{\alpha_t(1-\alpha_{t-1})}z_{t-2}+\sqrt{1-\alpha_t}z_{t-1}$可以参数重整化为只含一个随机变量$z$构成的$\sqrt{1-\alpha_t\alpha_{t-1}}z$的形式。
根据上面的公式我们可以发现，想象中我们添加了$T$次噪声，但实际上我们可以只通过对原图添加一次噪声就得到$t$时刻的图像。

根据以上推导过程，我们可以得到任意时刻的$x_t$都满足:

$$q(x_t|x_0)=\mathcal{N}(x_t;\sqrt{\bar\alpha_t}x_0,(1-\bar\alpha_t)\Iota) \tag{2-5}$$

这为我们后面的预测模型打下了基础。

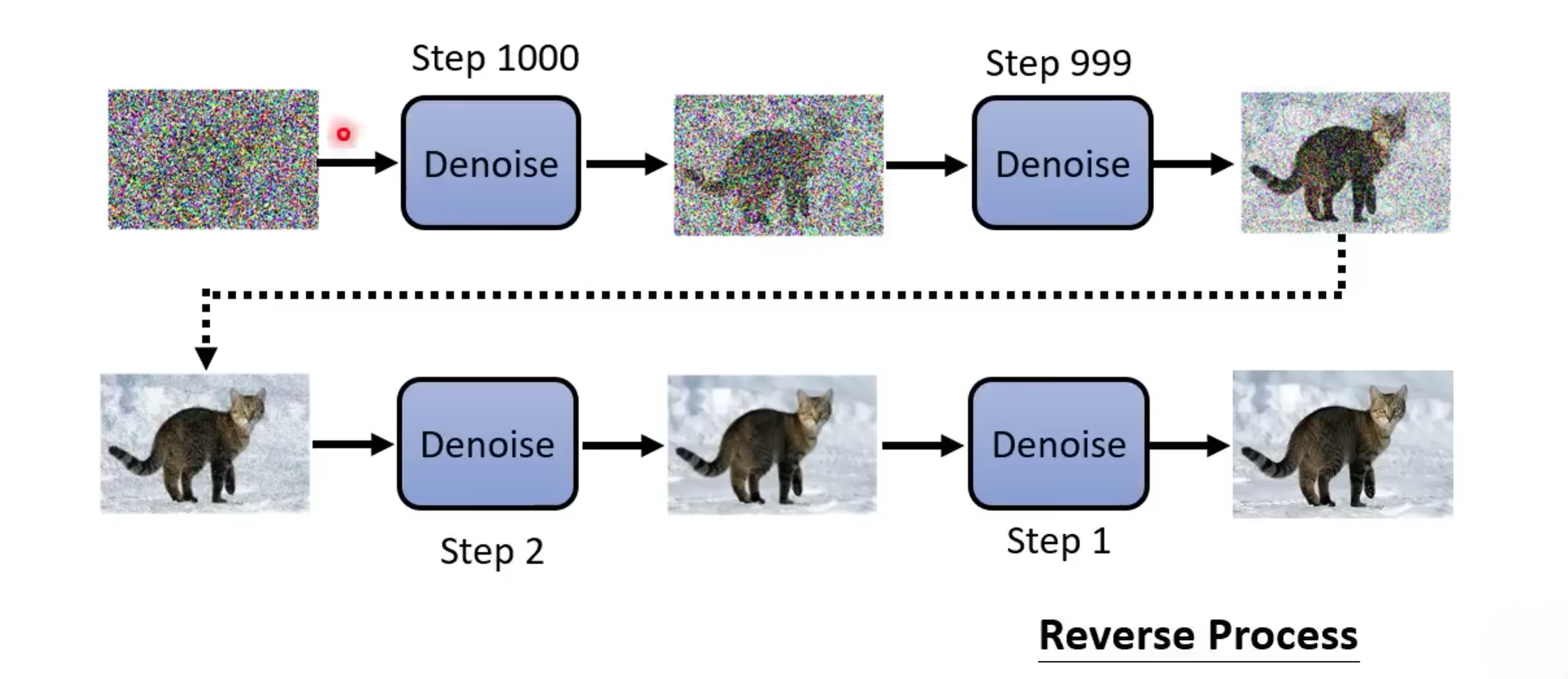
2.2 Diffusion逆向扩散过程（Reverse Process）

前面我们说到前向传播过程是一个向图片添加高斯噪声的过程，那么逆向传播过程就是为图片去噪的过程。

如果我们能够逐步得到逆转后的分布$q(x_{t-1}|x_t)$，就可以从完全的标准高斯分布$x_T \sim \mathcal{N}(0,\Iota)$还原出原图分布$x_0$.在已有的文献中已经证明了如果$q(x_t|x_{t-1})$满足高斯分布且$\beta_t$足够小，$q(x_{t-1}|x_t)$仍然是一个高斯分布。然而我们无法简单推断$q(x_{t-1}|x_t)$，因此我们使用深度学习模型（参数为$\theta$，目前主流是U-Net+attention的结构）去预测这样的一个逆向的分布$p_\theta$（类似VAE）：

$$\begin{align*} p_\theta(x_{0:T}) = p(x_T)\prod_{t=1}^Tp_\theta(x_{t-1}|x_t) \tag{2-6}\newline p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1};\mu_\theta(x_t,t),\sum_\theta(x_t,t)) \tag{2-7}\hspace{-1.54cm} \end{align*}$$

我们如何根据$x_t$图像反向得到$x_{t-1}$呢？我们已经知道$q(x_t|x_{t-1})$，那么我们就可以根据贝叶斯公式得到:

$$q(x_{t-1}|x_t)=q(x_t|x_{t-1})\frac{q(x_{t-1})}{q(x_t)} \tag{2-8}$$

但是在公式(2-8)中，$q(x_t)$和$q(x_{t-1})$是未知的，由公式(2-4)我们知道可以由$x_0$得到每一时刻的图像，所以我们可以得到：

$$\begin{align*} q(x_{t-1}|x_0) = \sqrt{\bar\alpha_{t-1}}x_0+\sqrt{1-\bar\alpha_{t-1}}z \tag{2-9}\newline q(x_t|x_0) = \sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}z \hspace{1.05cm} \tag{2-10}\newline q(x_t|x_{t-1},x_0) = \sqrt{\alpha_t}x_{t-1}+\sqrt{1-\alpha_t}z \tag{2-11} \end{align*}$$

那么公式(2-8)就可以化为：

$$q(x_{t-1}|x_t,x_0) = q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} \tag{2-12}$$

且：

$$q(x_{t-1}|x_t,x_0) = \mathcal{N}(x_{t-1};\tilde{\mu_t}(x_t,x_0),\tilde{\beta_t}\Iota) \tag{2-13}$$

根据高斯分布的概率密度函数：

$$\begin{align*} f(x) &= \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \\ &= \frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{1}{2}[\frac{1}{\sigma^2}x^2-\frac{2\mu}{\sigma^2}x+\frac{\mu^2}{\sigma^2}]} \tag{2-14} \end{align*}$$

我们就将公式(2-12)化为：

$$\begin{align*} q(x_{t-1}|x_t,x_0) &= q(x_t|x_{t-1},x_0)\frac{q(x_{t-1}|x_0)}{q(x_t|x_0)} \\ &\propto exp(-\frac{1}{2}(\frac{(x_t-\sqrt{\alpha_t}x_{t-1})^2}{\beta_t}+\frac{(x_{t-1}-\sqrt{\bar\alpha_{t-1}x_0})^2}{1-\bar\alpha_{t-1}}-\frac{(x_t-\sqrt{\bar\alpha_t}x_0)^2}{1-\bar\alpha_t})) \\ &= exp(-\frac{1}{2}((\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}})x_{t-1}^2-(\frac{2\sqrt{\alpha_t}}{\beta_t}x_t+\frac{2\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}x_0)x_{t-1}+C(x_t,x_0))) \tag{2-15} \end{align*}$$

再根据公式(2-14)的形式我们可以得到公式(2-13)中的$\tilde{\mu}(x_t,x_0)$和$\tilde{\beta_t}$

$$\begin{align*} \tilde{\beta_t} = 1/(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}})=\frac{1-\bar\alpha_{t-1}}{1-\bar\alpha_t}\beta_t \hspace{6.97cm}\tag{2-16}\newline \tilde{\mu_t}(x_t,x_0) = (\frac{\sqrt{\alpha_t}}{\beta_t}x_t+\frac{\sqrt{\bar\alpha_t}}{1-\bar\alpha_t}x_0)/(\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}) = \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_t}x_t+\frac{\sqrt{\bar\alpha_{t-1}}\beta_t}{1-\bar\alpha_t}x_0 \tag{2-17} \end{align*}$$

再根据公式(2-4)我们可以得到：

$$x_0 = \frac{1}{\sqrt{\bar\alpha_t}}(x_t-\sqrt{1-\bar\alpha_t}\bar{z_t}) \tag{2-18}$$

将公式(2-18)带入到公式(2-17)中可以得到：

$$\tilde\mu_t = \frac{1}{\sqrt{\alpha_t}}(x_t-\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}\bar{z_t}) \tag{2-19}$$

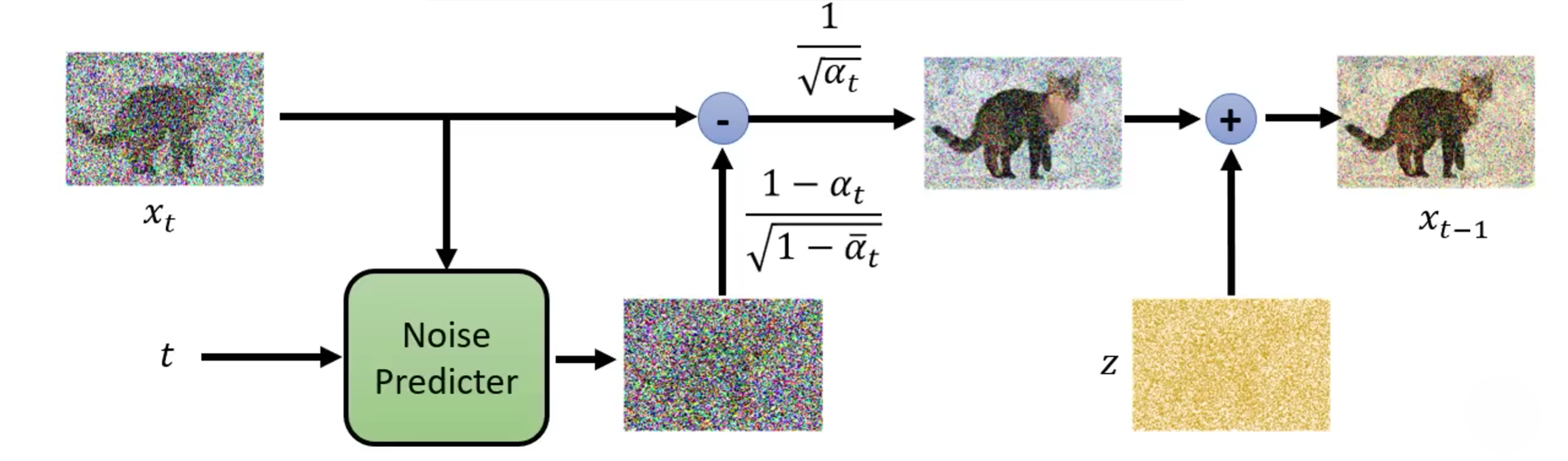
但是在论文中实现的DDPM与我们上面的计算还是有一些小小的不同：

所以按照论文中的伪代码，DDPM的一次降噪过程实际上有如下几步：

1. 将随机采样处的噪声图片$x_t$以及$t$传入Noise Predicter生成预测的噪声结果$\epsilon_\theta(x_t,t)$
2. 使用原图$x_t$减去预测噪声的$\frac{1-\alpha_t}{\sqrt{1-\bar\alpha_t}}$倍后再乘以$\frac{1}{\sqrt{\alpha_t}}$就可以得到比较干净的图了
3. 但是在DDPM中，这里又多了一步，那就是将得到的图再加上了一个$\sigma_t$倍的$z$，其中$z$也是从标准高斯分布中采样得到的噪声，然后得到了最终的图片。
   对于这里为什么要加上$\sigma_tz$，根据李宏毅老师说的就是为了引入随机性，只有引入随机性结果才会好，实验结果也证明了这点。
   ChatGPT也是这样说的：
   

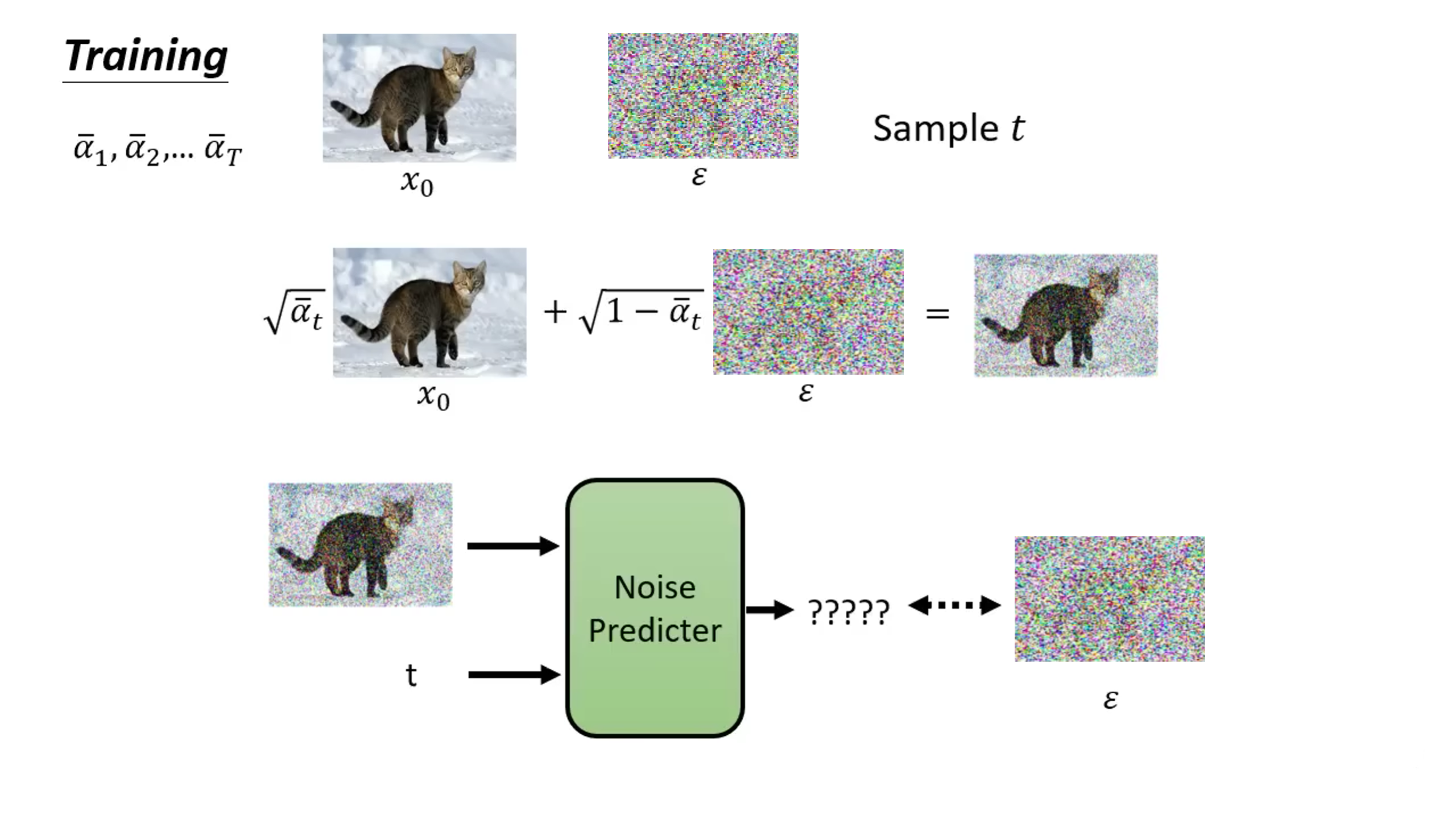
2.3 Training过程

Training过程如下：

在训练过程中，我们首先从分布$q(x_0)$中采样出一个干净的图片$x_0$，然后从$\{1,..,T\}$中随机采样一个$t$用于控制原图与添加的噪声的比例，最后再从标准正态分布中随机采样一个噪声$\epsilon$，这样就完成了采样的工作。
然后我们通过$x_0$和$\epsilon$生成有噪声的图$x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon$，之后我们将$x_t$和$t$输入到一个噪声预测器中，预测得到一个噪声$\epsilon_\theta(\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon,t)$，然后将预测得到的噪声与我们的原噪音$\epsilon$进行比较，具体过程如下图所示：

根据上面的分析，我们的目标就是尽可能减小原噪声$\epsilon$与预测噪声$\epsilon_\theta$的差别，所以我们的损失函数就是：

$$\mathcal{L}_{simple}(\theta) = \char"1D53C_{t,x_0,\epsilon}[||\epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon,t)||^2]$$

三、代码实现

3.1 数据集选择

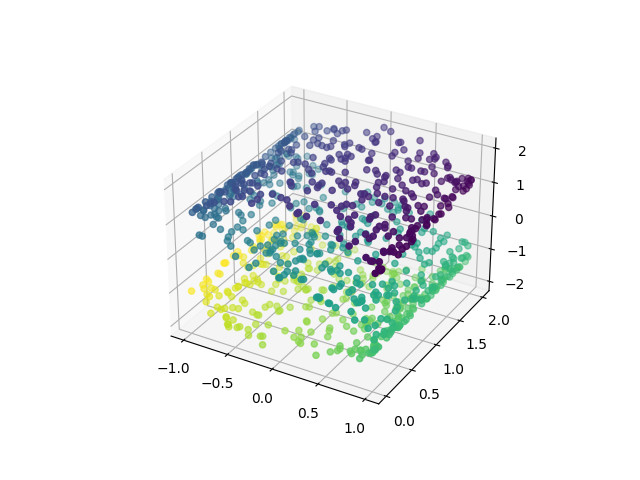
简单起见，我们使用sklearn库中的make_s_curve函数来生成三维S曲线数据集。
该make_s_curve函数使用数学公式生成S曲线，并返回包含生成的数据和相应目标值的元组。生成的数据是二维NumPy数组(n_samples, 3)，其中n_samples为样本数，每一行代表三维空间中的一个点。目标值是一个一维NumPy形状数组(n_samples,)，其中包含S曲线中每个点的颜色代码（介于 0 和 1 之间）。
使用make_s_curve函数生成S曲线的示例:

# 生成S-curve数据集
from sklearn.datasets import make_s_curve
import matplotlib.pyplot as plt
 
X, y = make_s_curve(n_samples=1000)

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=y)
plt.show()

生成的3D数据集可视化如下：

我们使用make_s_curve函数生成一个包含10000个点的数据集。为了方便起见。我们只取s_curve的第0维和第2维，相当于s_curve的一个截面。

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_s_curve
import torch

s_curve, _ = make_s_curve(10**4, noise=0.1)
s_curve = s_curve[:,[0,2]]/10.0  # 每个点取第0维和第2维, 再除以10
print("shape of s:", np.shape(s_curve))

data = s_curve.T
fig,ax = plt.subplots()
ax.scatter(*data,color='orange',edgecolor='white');
ax.axis('off')

dataset = torch.Tensor(s_curve).float()  # 将S曲线构建成一个张量
plt.show()

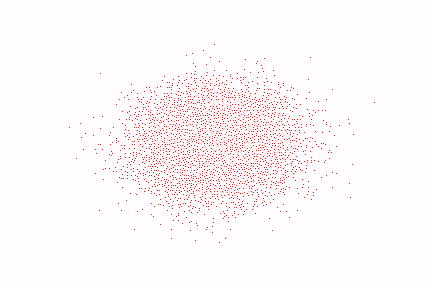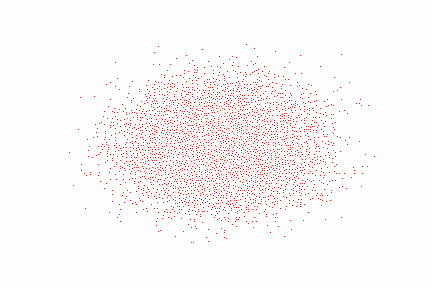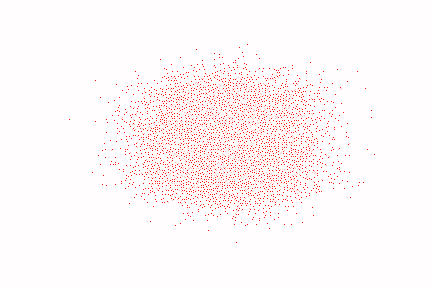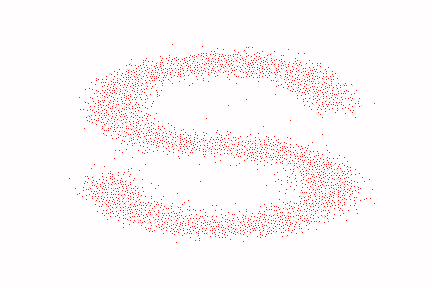
最终生成的数据集如下所示：

3.2 计算超参数

在计算超参数之前，我们先来总结一下我们都有哪些超参数需要计算：

1. 首先是$\beta_t$，它控制了添加的噪声的比例。这里我们取$\beta_t \in [0.00001, 0.005]$。
2. 然后是$\alpha_t$以及$\bar\alpha$，其中$\alpha_t=1-\beta_t，\bar\alpha=\prod_{i=1}^T\alpha_i$。

所以我们最后的代码就是：

# 计算所需要的超参数
num_steps = 100  # 设置步长用来生成beta

# 生成beta
betas = torch.linspace(-6, 6, num_steps)  # β从-6到6均匀取100个值
betas = torch.sigmoid(betas)*(0.5e-2 - 1e-5)+1e-5  # 将β的值全部控制在[1e-5，0.5e-2]之间

# 计算alpha
alphas = 1 - betas  # α_t=1-βt
alphas_prod = torch.cumprod(alphas,0)  # α_t的累乘
alphas_prod_p = torch.cat([torch.tensor([1]).float(), alphas_prod[:-1]], 0)  # α^t-1d的累乘
alphas_bar_sqrt = torch.sqrt(alphas_prod)  # 根号下α_t的累乘
one_minus_alphas_bar_log = torch.log(1 - alphas_prod)  # 1-α_t的累乘再取log
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)  # 根号下1-α_t的累乘

# 使用assert来确保所有相关张量的形状相同，避免后续计算中出现形状不匹配的问题
assert alphas.shape==alphas_prod.shape==alphas_prod_p.shape==alphas_bar_sqrt.shape==one_minus_alphas_bar_log.shape==one_minus_alphas_bar_sqrt.shape
print("all the same shape",betas.shape)

其中：

• torch.linspace(start, end, steps=100, out=None, dtype=None, layout=torch.strided, device=None, requires_grad=False): 其作用是返回一个tensor张量，这个张量包含了从start到end的等距的steps个数据点；
• torch.sigmoid()：sigmoid公式：$f(x)=\frac{1}{1+e^{-x}}$。因为sigmoid函数的值域为[0,1]，所以sigmoid(betas)可以将$\beta$的值平滑地压缩到[0,1]之间，再通过乘以(0.5e-2 - 1e-5) + 1e-5将$\beta$的值放缩到[1e-5,0.5e-2]之间。
• alphas_prod_p = torch.cat([torch.tensor([1]).float(), alphas_prod[:-1]], 0)：torch.tensor([1]).float()：创建一个标量1（对应α_0时的累乘值，通常初始状态下α_0设为1）；alphas_prod[:-1]：取alphas_prod除去最后一个元素的部分，即[α_1 * α_2 * … * α_t]；torch.cat([…], 0)：将标量1和去掉最后一个元素的alphas_prod拼接在一起。
  假设alphas_prod是[α_1, α_1 * α_2, α_1 * α_2 * α_3, …, α_1 * α_2 * … * α_t]。那么alphas_prod_p就是[1, α_1, α_1 * α_2, α_1 * α_2 * α_3, …, α_1 * α_2 * … * α_{t-1}]（即去掉最后一个元素，前面拼上一个1）。

3.3 前向传播过程

前向扩散过程中，根据公式：

$$x_t = \sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\bar{z_t} \tag{3-1}$$

我们可以知道可以基于$x_0$得到任意时刻$t$的值$x_t$。
代码如下：

# 计算任意时刻的x采样值，基于x_0和重参数化技巧
def q_x(x_0, t):

    noise = torch.randn_like(x_0)  # noise为从正态分布中采样的随机噪声，也就是公式中的z_t
    
    alphas_t = alphas_bar_sqrt[t]  # 根号下bar{α_t}
    alphas_1_m_t = one_minus_alphas_bar_sqrt[t]  # 根号下(1-bar{α_t})
    return (alphas_t * x_0 + alphas_1_m_t * noise) # 在x[0]的基础上添加噪声

注：torch.randn_like()：返回一个与输入张量大小相同的张量，其中填充了均值为0方差为1的正态分布的随机值。

3.4 演示原始数据分布加噪100步后的效果

num_shows = 20
fig,axs = plt.subplots(2, 10, figsize=(28,3))  # 创建一个2行10列的子图 (即20个子图)，每个子图大小为28x3。fig是图像对象，axs是子图的坐标轴数组
plt.rc('text',color='black')

#共有10000个点，每个点包含两个坐标
#生成100步以内每隔5步加噪声后的图像
for i in range(num_shows):
    # 用于确定当前的子图位置。j确定当前是第几行，k确定是第几列
    j = i // 10
    k = i % 10
    q_i = q_x(dataset, torch.tensor([i*num_steps//num_shows])) # 生成t时刻的采样数据
    axs[j,k].scatter(q_i[:,0], q_i[:,1], color='green', edgecolor='white')
    axs[j,k].set_axis_off()
    axs[j,k].set_title('$q(\mathbf{x}_{'+str(i*num_steps//num_shows)+'})$')

plt.show()

效果如下：

通过图像我们可以看出经过不断加噪之后图像会变得越来越趋于纯噪声图片。

3.5 编写拟合逆扩散过程高斯分布的模型

简单起见，我们使用一个简单的多层感知机(MLP)来实现模型：

import torch
import torch.nn as nn

class MLPDiffusion(nn.Module):
    
    def __init__(self, n_steps, num_units=128):
        super(MLPDiffusion,self).__init__()
        
        self.linears = nn.ModuleList(
            [
                nn.Linear(2, num_units),
                nn.ReLU(),
                nn.Linear(num_units,num_units),
                nn.ReLU(),
                nn.Linear(num_units,num_units),
                nn.ReLU(),
                nn.Linear(num_units,2),
            ]
        )
        self.step_embeddings = nn.ModuleList(
            [
                nn.Embedding(n_steps,num_units),  # [100,128]
                nn.Embedding(n_steps,num_units),
                nn.Embedding(n_steps,num_units),
            ]
        )
        
    def forward(self, x, t):
        for idx, embedding_layer in enumerate(self.step_embeddings):
            t_embedding = embedding_layer(t)  # 选第t步的Embedding
            x = self.linears[2*idx](x)  # 先送入Linear层
            x += t_embedding  # 加上Embedding
            x = self.linears[2*idx+1](x)  # 再送入ReLU层
        
        x = self.linears[-1](x)  # 最后一个Linear层, 输出为[10000, 2]
        return x

这里我们构建了一个7层的MLP模型（虽然MLPDiffusion中step_embeddings也定义了3个时间嵌入层(nn.Embedding)，但这些不属于标准的"网络层"如线性层或激活层）。它们用于引入时间步的信息，并在每次计算中与线性层的输出相加，而不是单独作为一层计算）：

1. Linear(2, num_units)：从2维输入映射到128维。
2. ReLU()：非线性激活。
3. Linear(num_units, num_units)：128维到128维的映射。
4. ReLU()：非线性激活。
5. Linear(num_units, num_units)：再一次128维到128维的映射。
6. ReLU()：非线性激活。
7. Linear(num_units, 2)：输出层，128维压缩回2维。

注：embedding层可以引入时间步的信息，通过时间步嵌入，模型能根据当前的时间步 t 调整对数据的处理策略。例如：早期时间步时，模型可能只需要做少量修复，因为数据仍然接近原始状态；而晚期时间步时，模型需要更复杂的操作来逆转严重污染的数据。在扩散模型中，时间步嵌入让模型理解数据如何从无噪声逐渐变为噪声化的过程，并帮助模型逐步去噪。

3.6 编写损失函数

在训练过程中，我们通过输入加噪后的图片$x_t=\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon$和$t$预测出噪声$\epsilon_\theta$，再通过预测得到的噪声与原噪声对比获得损失。

所以我们的损失函数就是:

$$\mathcal{L}_{simple}(\theta) = \char"1D53C_{t,x_0,\epsilon}[||\epsilon-\epsilon_\theta(\sqrt{\bar\alpha_t}x_0+\sqrt{1-\bar\alpha_t}\epsilon,t)||^2]$$

def diffusion_loss_fn(model, x_0, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, n_steps):
    # 对任意时刻t进行采样计算loss
    
    batch_size = x_0.shape[0]  # 获取输入图像x_0的batch_size
    
    # 对一个batchsize样本生成随机的时刻t, 覆盖到更多不同的t
    t = torch.randint(0, n_steps, size=(batch_size//2,))  # 在0到n_steps-1的范围内生成batch_size/2个随机数（表示时间步t）
    t = torch.cat([t, n_steps-1-t], dim=0)  # 生成的t值会与n_steps-1-t进行拼接，确保生成的时间步尽量不重复，并增加多样性
    t = t.unsqueeze(-1)  # 增加一个维度，使其形状变为(batch_size, 1)
    
    # x0的系数
    a = alphas_bar_sqrt[t]  # 根号下bar{α_t}
    
    # eps的系数
    aml = one_minus_alphas_bar_sqrt[t]  # 根号下(1-bar{α_t})
    
    # 生成随机噪音eps
    e = torch.randn_like(x_0)  
    
    # 计算输入x_t：根号下bar{α_t}*x_0+根号下(1-bar{α_t})*eps
    x = x_0 * a+e * aml  
    
    # 计算t时刻的随机噪声预测值
    output = model(x, t.squeeze(-1))  # 模型预测的是噪声, 噪声维度与x0一样大, [10000,2]
    
    # 与真实噪声一起计算误差，求平均值
    return (e - output).square().mean()

3.7 编写逆扩散采样函数（inference过程）

根据论文中的采样过程：

我们可以根据$x_t$和$t$计算得到$x_{t-1}$，然后一步一步往前推，直到将图像还原到$x_0$。

def p_sample_loop(model, shape, n_steps, betas, one_minus_alphas_bar_sqrt):
    # 从x[T]恢复x[T-1]、x[T-2]、...x[0]
      
    cur_x = torch.randn(shape)  # 随机噪声, 对应x_t
    x_seq = [cur_x]  # x[T]、x[T-1]、x[T-2]、...x[0]
    for i in reversed(range(n_steps)):
        cur_x = p_sample(model, cur_x, i, betas, one_minus_alphas_bar_sqrt)
        x_seq.append(cur_x)
    return x_seq


def p_sample(model, x, t, betas, one_minus_alphas_bar_sqrt):
    # 从x[T]采样t时刻的重构值，也就是将x_t还原为x_{t-1}

    t = torch.tensor([t])
    coeff = betas[t] / one_minus_alphas_bar_sqrt[t]  # 模型输出的系数：β_t/根号下(1-bar{α_t}) = 1-α_t/根号下(1-bar{α_t})
    eps_theta = model(x, t)  # 模型的输出: ε_θ(x_t, t)
        
    # (1/根号下α_t)*(x_t-(1-α_t/根号下(1-bar{α_t}))*ε_θ(x_t, t))
    mean = (1/(1-betas[t]).sqrt())*(x-(coeff*eps_theta))  
    
    z = torch.randn_like(x)  # 对应公式中的z
    sigma_t = betas[t].sqrt()  # 对应公式中的σ_t
    
    sample = mean + sigma_t * z 
    
    return (sample)

3.8 训练模型

训练模型并打印loss及中间重构效果：

print('Training model...')
batch_size = 128
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)
num_epoch = 4000
plt.rc('text',color='blue')

model = MLPDiffusion(num_steps)  # 输出维度是2，输入是x和step
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3) 

for t in range(num_epoch):
    for idx, batch_x in enumerate(dataloader):
        loss = diffusion_loss_fn(model, batch_x, alphas_bar_sqrt, one_minus_alphas_bar_sqrt, num_steps)  # 计算损失
        optimizer.zero_grad()  # 梯度清零
        loss.backward()  # 损失回传
        torch.nn.utils.clip_grad_norm_(model.parameters(),1.)  # 梯度裁剪
        optimizer.step()  
        
    if(t % 100 == 0):
        print(loss)  # 每100个epoch打印一次loss
        x_seq = p_sample_loop(model, dataset.shape, num_steps, betas, one_minus_alphas_bar_sqrt)
        
        fig, axs = plt.subplots(1, 10, figsize=(28,3))
        for i in range(1, 11):
            cur_x = x_seq[i*10].detach()
            axs[i-1].scatter(cur_x[:,0],cur_x[:,1],color='red',edgecolor='white');
            axs[i-1].set_axis_off();
            axs[i-1].set_title('$q(\mathbf{x}_{'+str(i*10)+'})$')

效果如下（由于图像过多，这里只截取了epoch为0，1000，2000，3000，4000时的图像）：





根据图象我们可以看到，随着epoch的不断增加，图像的去噪效果越来越好。

3.9 动态可视化

import io
from PIL import Image

# 前向过程
imgs = []
for i in range(100):
    plt.clf()
    q_i = q_x(dataset,torch.tensor([i]))
    plt.scatter(q_i[:,0],q_i[:,1],color='red',edgecolor='white',s=5);
    plt.axis('off');
    
    img_buf = io.BytesIO()
    plt.savefig(img_buf,format='png')
    img = Image.open(img_buf)
    imgs.append(img)

# 逆向过程
reverse = []
for i in range(100):
    plt.clf()
    cur_x = x_seq[i].detach()
    plt.scatter(cur_x[:,0],cur_x[:,1],color='red',edgecolor='white',s=5);
    plt.axis('off')
    
    img_buf = io.BytesIO()
    plt.savefig(img_buf,format='png')
    img = Image.open(img_buf)
    reverse.append(img)

imgs = imgs
imgs[0].save("diffusion_qian.gif", format='GIF', append_images=imgs, save_all=True, duration=100, loop=0)

imgs = reverse
imgs[0].save("diffusion_ni.gif", format='GIF', append_images=imgs, save_all=True, duration=100, loop=0)

前向过程：

逆向过程：

参考资料：
[1] Denoising Diffusion Probabilistic Models
[2] 扩散模型 - Diffusion Model【李宏毅2023】
[3] Probabilistic Diffusion Model概率扩散模型理论与完整PyTorch代码详细解读
[4] 由浅入深了解Diffusion Model
[5] 百度百科